JCA modelとBiot Parameterについて
Biot Parameterとその定義
ここではBiot parameterと呼ばれる,多孔質材内部の空隙の量や形状を表すパラメータを解説する。
Johnson-Champoux-Allard(-Lafarge) modelは内部流体の特性をこれらのパラメータにより表すモデルである。
・多孔度 (Porosity : \(\phi\) [])
多孔度は多孔質材料の見かけの体積(\(V_\mathrm{a}\))に対する空隙部分の体積(\(V_\mathrm{b}\))の比で定義される。
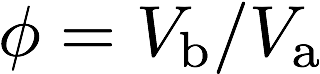
また,多孔度は骨格を形成する材料の物質密度 \(\rho_\mathrm{s}\),及び多孔質材料の嵩密度 \(\rho_\mathrm{b}\)より
以下のように表すことができる。
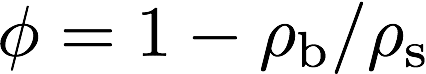
・迷路度 (Tortuosity : \(\alpha_\infty\) [])
迷路度は円筒管モデルにおいては円筒管の傾きを表すパラメータである。一般的には超音波領域における空気に対する多孔質材料の屈折率として以下のように定義される。
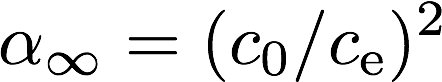
ここで,\(c_0\)は空気中の音速,\(c_\mathrm{e}\)は多孔質材料内部の空気中の音速である。
・流れ抵抗 (Airflow Resistivity : \(\sigma\) [Ns/m\(^4\)])
流れ抵抗は材料内部の空気の流れにくさを表すパラメータで,特に低音域における粘性抵抗に関連する。多孔質材料に一定流速\(U\)を流した際に生じる,材料表裏の音圧差\(\Delta p\)から以下のように定義される。
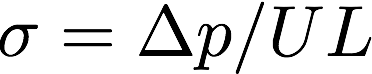
Lは材料厚さで,単位長さあたりに受ける抵抗を表している。
・粘性特性長 (Viscous Characteristic Length : \(\Lambda\) [m])
粘性特性長は実効密度の高音域における挙動を表すためJohnsonらにより導入されたパラメータである。細孔内における非圧縮性・非粘性の定常流に対し,以下のように定義される。

\(v(\mathbf{r})\)は細孔内の流速,\(\Omega\)は多孔質材の代表体積内の空気領域,\(\Gamma\)は多孔質材の代表体積内の境界面(骨格表面)を表す。
・熱浸透率 (Thermal Permeability : \(k^\prime_0\) [m\(^2\)])
熱浸透率は粘性と熱伝導の相似性を考慮し,複素体積弾性率の低音域における挙動を表すためLafargeらにより導入されたパラメータである(Johnson-Champoux-Allard-Lafarge model)。熱浸透率は計測が容易では無く,また多孔質材料内部では粘性が主要な減衰効果であることから,次式に置き換えたJohnson-Champoux-Allard modelがよく用いられる。

上式は円筒管における熱浸透率と次に示す熱的特性長の関係である。
・熱的特性長 (Thermal Characteristic Length : \(\Lambda^\prime\)[m])
熱的特性長は複素体積弾性率の高音域における挙動を表すためChampouxらにより導入されたパラメータである。熱的特性長は多孔質材の代表体積内の空気の体積と,骨格の表面積の比として以下のように定義される。

尚,粘性・熱的特性長の定義式における係数"2"は,円筒管においてそれぞれが円筒の直径と一致させるために設定された係数である。
その他のパラメータ
・動粘性係数 (viscosity : \(\eta\)[Ns/m\(^2\)] )
20℃の空気で\(1.8\times10^{-5}\)[Ns/m\(^2\)]である。
・比熱比 (heat capacity ratio : \(\gamma\)[] )
定圧熱容量と定積熱容量の比で,空気では1.4である。
・プラントル数 (Prandtl Number : \(N_\mathrm{pr}\)[] )
動粘性係数と温度拡散度の比で,空気では0.71である。
・大気圧 (Static Pressure : \(P_0\)[Pa] )
空気では101.3 [kPa]である。
JCA modelにおける実効密度
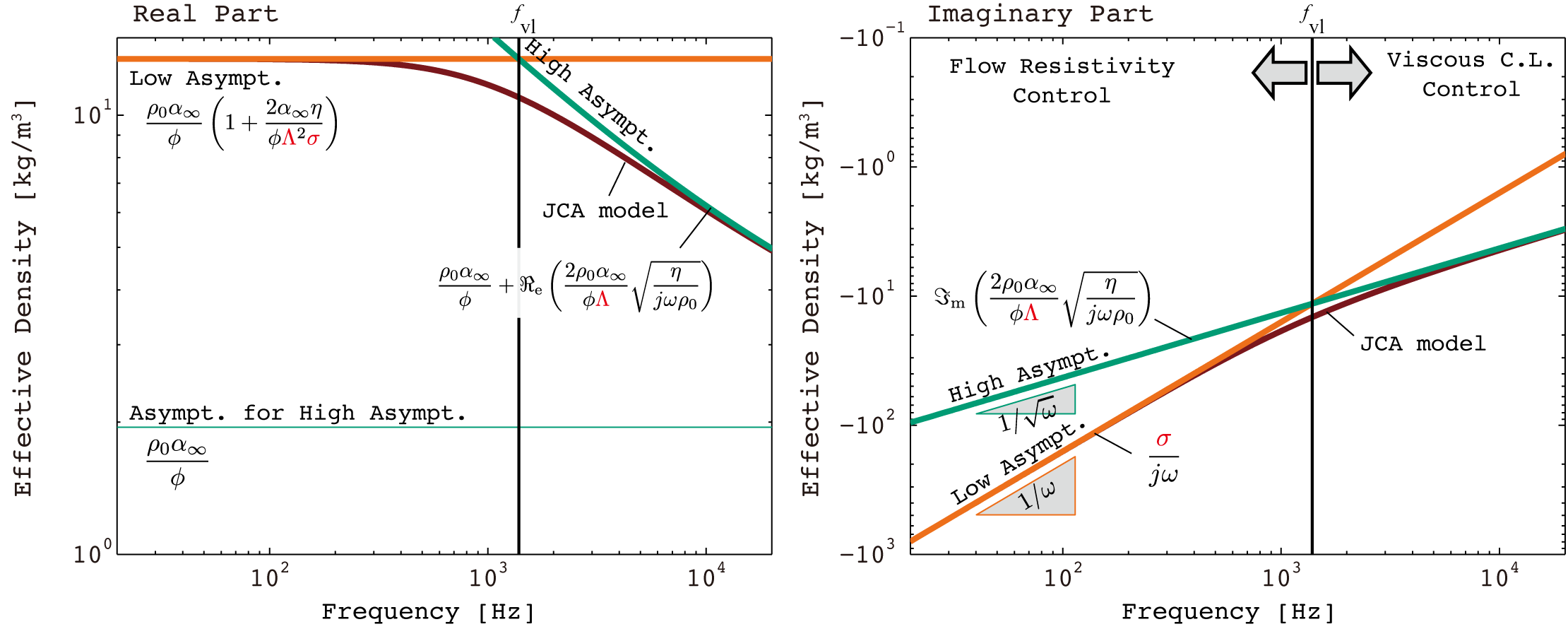
図.1 JCA modelによる実効密度の実部と虚部. 入力パラメータ \((\phi, \alpha_\infty, \sigma, \Lambda) = (0.99, 1.6, 1.0\times10^5, 1.0\times10^{-6})\).
低音域・高音域の漸近線
Johnsonらは低音域,高音域の漸近挙動がそれぞれ以下のように書けることを示している。
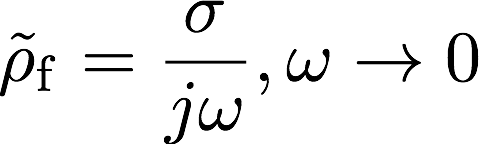
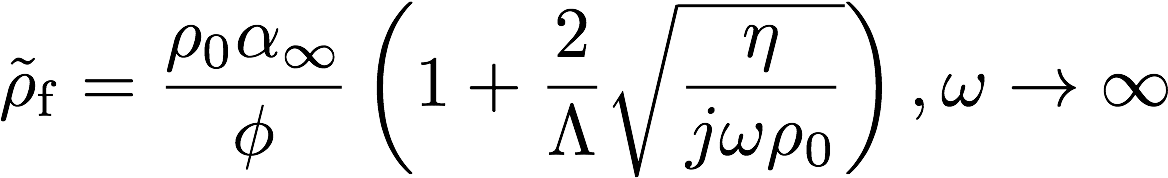
※これらはそれぞれ,円筒管モデルにおけるRayleighのNarrow tube, KirchhoffのWide tubeの近似に相当するものと解釈できる。
Johnson-Allard model
Johnsonらは上記の漸近挙動を示す単純なモデルとして以下の式を提案している。

また,二つの漸近線の交差する周波数は,粘性減衰のメカニズムを把握する上で非常に重要である。実効密度では実部・虚部ともに遷移周波数は以下のように与えられる。

尚,JCA modelにおける遷移周波数付近の実効密度の挙動については物理的な根拠はない。
JCA modelにおける体積弾性率

図.2 JCA modelによる体積弾性率の逆数の実部と虚部. 入力パラメータ \((\phi, \Lambda^\prime, k^\prime_0) = (0.99, 1.0\times10^{-4}, \phi {\Lambda^\prime}^2/8)\).
低音域・高音域の漸近線
Lafargeらは低音域の漸近挙動を以下のように示している。

また,Champouxらは高音域の漸近挙動を以下のように示している。

複素体積弾性率の実部は低音域では等温過程,高音域では断熱過程の体積弾性率に漸近する。
Johnson-Champoux-Allard-Lafarge model
Champoux, Lafargeらは上記の漸近挙動を示す単純なモデルとして以下の式を提案している。
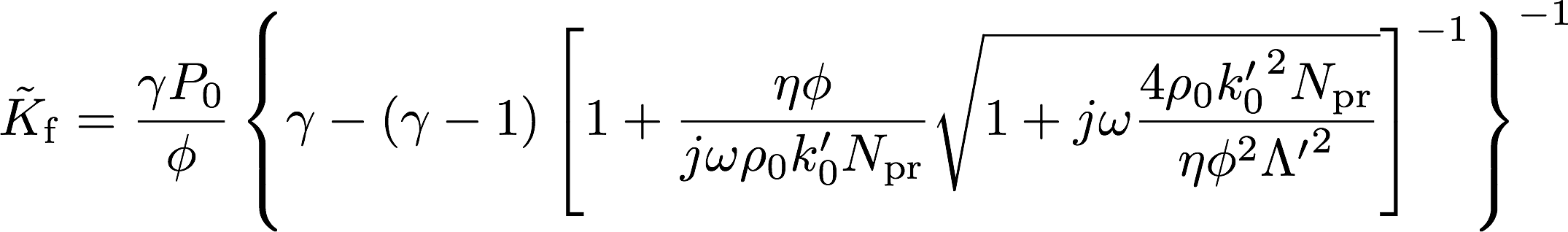
Johnson-Champoux-Allard model
先述のように,熱浸透率を\(k^\prime_0 = \phi {\Lambda^\prime}^2/8\)とおいたモデルがJCA modelである。
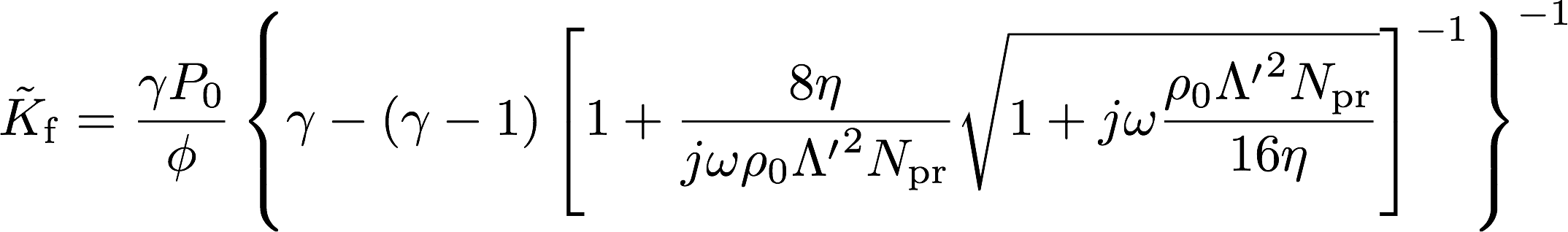
体積弾性率はその逆数の虚部が熱伝導減衰を表す。実効密度と同様に,二つの漸近線の交差する周波数は内部流体の状態変化や,熱伝導減衰メカニズムを把握する上で重要である。体積弾性率の逆数では遷移周波数は実部・虚部で異なり,それぞれ以下のように与えられる。
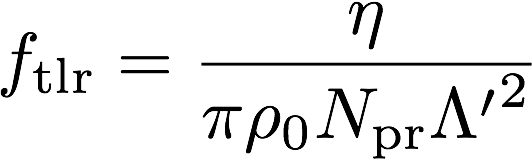
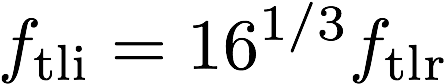
尚,JCAL, JCA modelにおける遷移周波数付近の複素体積弾性率の挙動については物理的な根拠はない。
参考文献
[1] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402[2] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979
[3] D. Lafarge, P. Lemarinier, J. F. Allard and V. Tarnow, Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp 1995-2006.
[4] Fellar Z.E.A, et.al, "Transient Acoustic Wave Propagation in Porous Media", Open Access, http://www.intechopen.com/books/modeling-and-measurement-methods-for-acoustic-waves-and-for-acoustic-microdevices/transient-acoustic-wave-propagation-in-porous-media