Miki modelとそのParameterについて

Parameterとその定義

Miki modelでは以下の3つのパラメータが用いられる。

・多孔度 (Porosity : \(\phi\) [])

多孔度は多孔質材料の見かけの体積(\(V_\mathrm{a}\))に対する空隙部分の体積(\(V_\mathrm{b}\))の比で定義される。



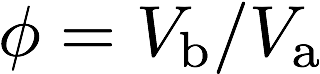
また，多孔度は骨格を形成する材料の物質密度 \(\rho_\mathrm{s}\)，及び多孔質材料の嵩密度 \(\rho_\mathrm{b}\)より 以下のように表すことができる。

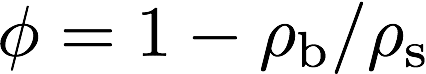
・迷路度 (Tortuosity : \(\alpha_\infty\) [])

迷路度は円筒管モデルにおいては円筒管の傾きを表すパラメータである。一般的には超音波領域における空気に対する多孔質材料の屈折率として以下のように定義される。



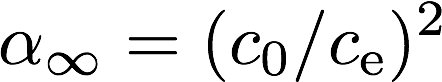
ここで，\(c_0\)は空気中の音速，\(c_\mathrm{e}\)は多孔質材料内部の空気中の音速である。

・流れ抵抗 (Airflow Resistivity : \(\sigma\) [Ns/m\(^4\)])

流れ抵抗は材料内部の空気の流れにくさを表すパラメータで，特に低音域における粘性抵抗に関連する。多孔質材料に一定流速\(U\)を流した際に生じる，材料表裏の音圧差\(\Delta p\)から以下のように定義される。



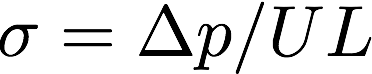
Lは材料厚さで，単位長さあたりに受ける抵抗を表している。

Miki model

Miki modelは円筒管内部音場の等価回路を基に，種々の多孔質材の実測値から構築された経験モデルである。ここでは，時間項として\(e^{j\omega t}\)を採用すると，Miki modelでは特性インピーダンス，複素波数が以下のように与えられる。

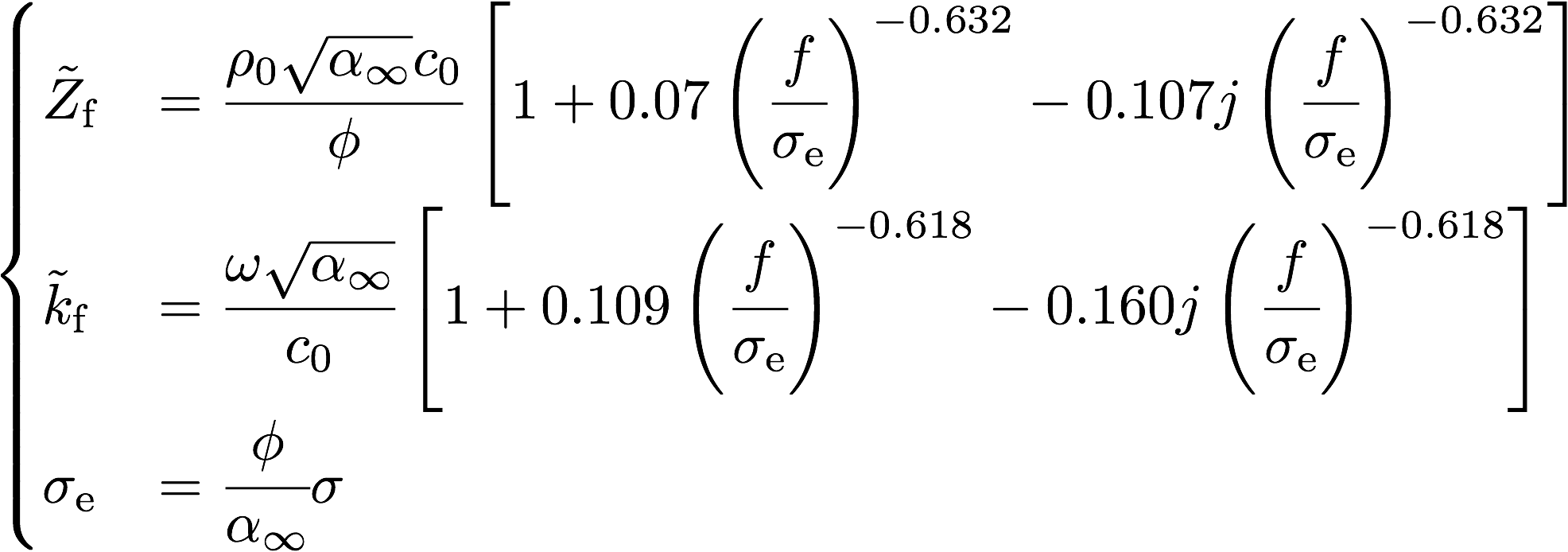
適用推奨周波数について

Miki modelの基となったDelany-Bazley modelでは以下の適用推奨範囲を示している。

\(0.01 < f/\sigma < 1.00\)

Delany-Bazley modelでは\(0.01 < f/\sigma \)の範囲で適用した際，表面インピーダンスの実部が負になる場合があり，物理的に無意味な値となってしまう。 Miki model では\(0.01 < f/\sigma_e \)の範囲でもこのような値をとることは無いが，その値の妥当性については十分検証されていないことに注意が必要である。

参考文献

[1] Miki Y., Acoustical properties of porous materials - Modifications of Delany-Bazley models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 19-24
[2] Miki Y., Acoustical properties of porous materials - Generalization of empirical models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 25-28