多孔質材の垂直入射吸音率の計算法
表面インピーダンスと垂直入射吸音率
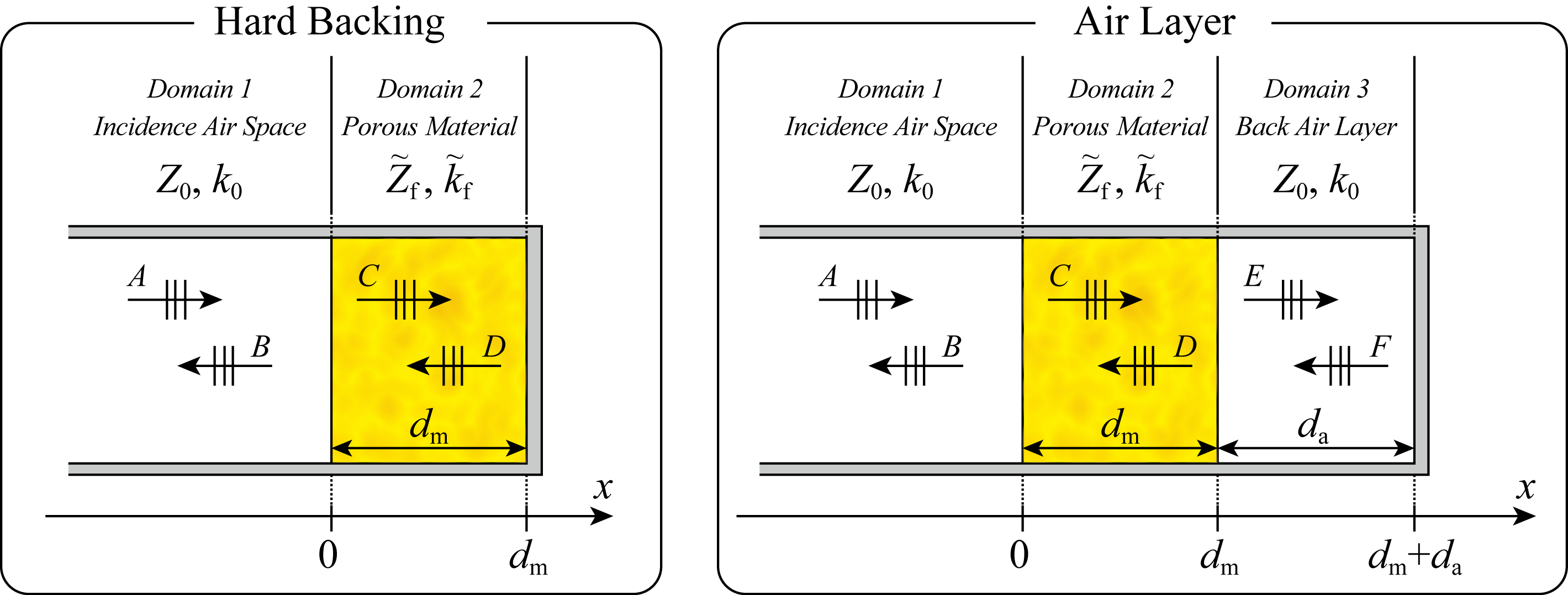
図.1 音響管問題
後壁密着条件における材料表面インピーダンスは以下のように与えられる。
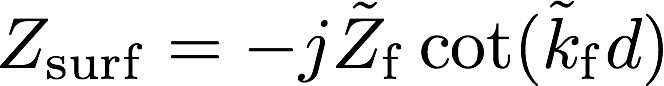・・・(1)
導出
-
領域1, 2で音圧，粒子速度の一般解は以下のように書ける。
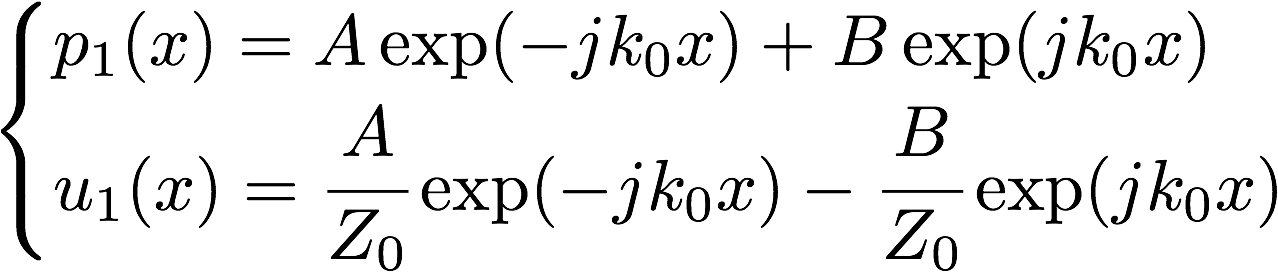
以下の3つの境界条件を考える。
1. 剛境界条件 : \(u_2(d) = 0\)
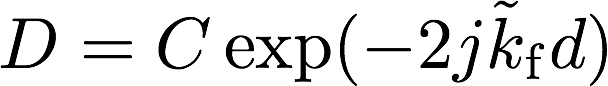・・・(3)
2. 音圧の連続 : \(p_1(0) = p_2(0)\)
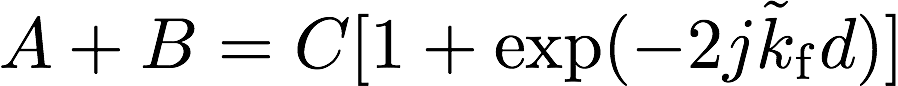・・・(4)
3. 粒子速度の連続 : \(u_1(0) = u_2(0)\)
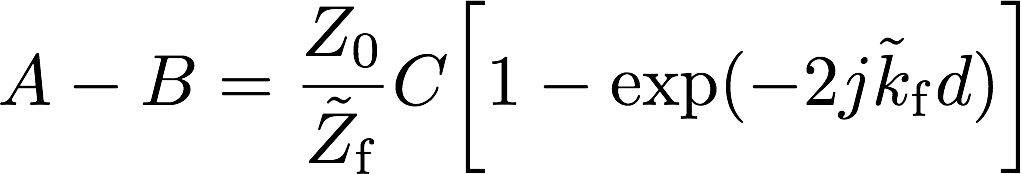・・・(5)
●材料表面の比音響インピーダンス
材料表面(\(@x = 0\))での比音響インピーダンスは式(4), (5)を用いて以下のように表せる。
背後空気層条件における材料表面インピーダンスは以下のように与えられる。
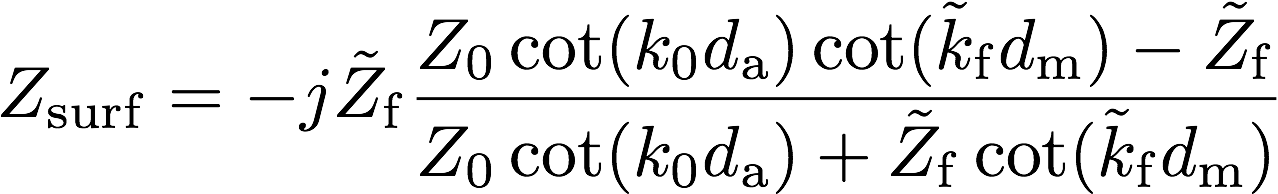・・・(2)
導出
-
領域1, 2, 3で音圧，粒子速度の一般解は以下のように書ける。
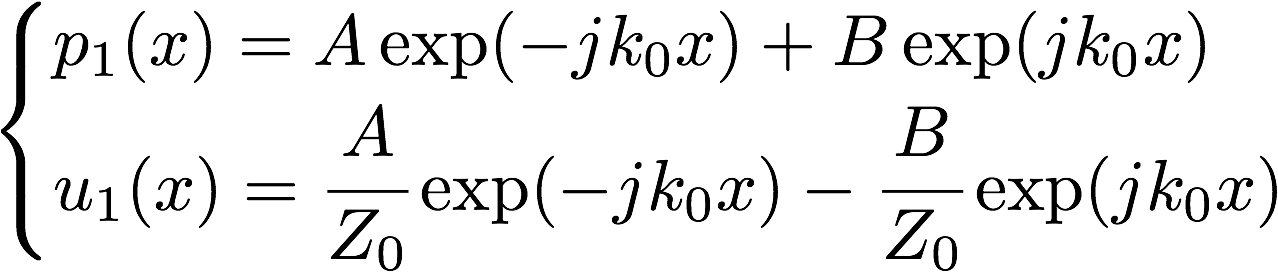
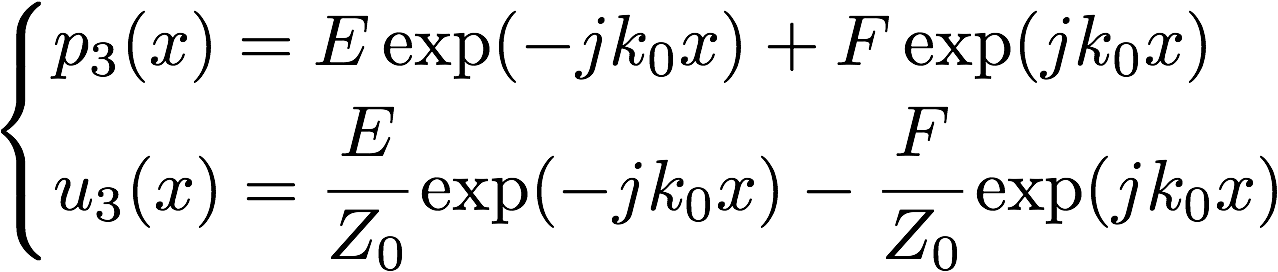
以下の5つの境界条件を考える。
1. 剛境界条件 : \(u_3(d_\mathrm{m} + d_\mathrm{a}) = 0\)
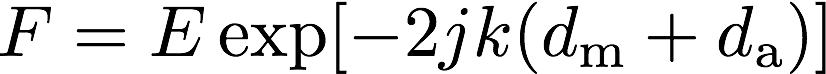・・・(6)
2. 音圧の連続 : \(p_1(0) = p_2(0)\)
p_1(0) = p_2(0)，及び式(3)より
・・・(7)
3. 粒子速度の連続 : \(u_1(0) = u_2(0)\)
u_1(0) = u_2(0)，及び式(3)より
・・・(8)
4. 音圧の連続 : \(p_2(d_\mathrm{m}) = p_3(d_\mathrm{m})\)
p_2(0) = p_3(0)，及び式(6)より
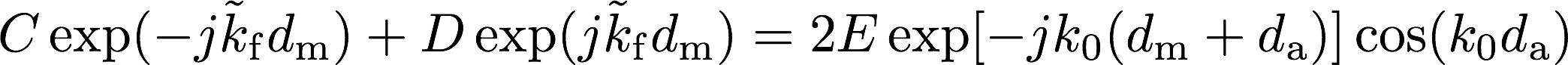・・・(9)
5. 粒子速度の連続 : \(u_2(d_\mathrm{m}) = u_3(d_\mathrm{m})\)
u_2(0) = u_3(0)，及び式(6)より
・・・(10)
●材料表面の比音響インピーダンス
式(9), (10)より係数C, Dは以下のように表せる。
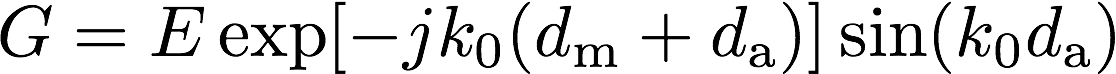
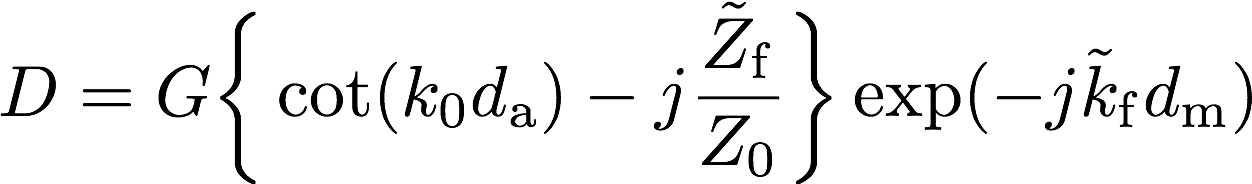
材料表面(@x = 0)での比音響インピーダンスは式(7), (8), (9), (10)を用いて以下のように表せる。
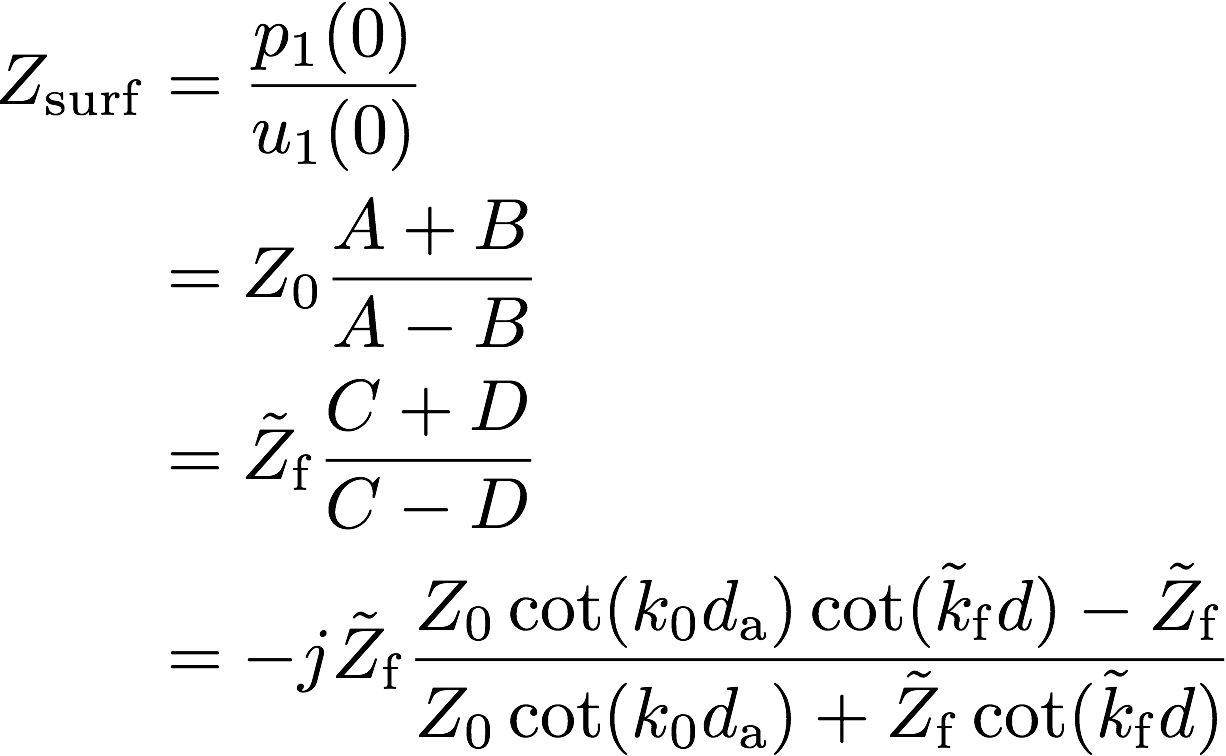
d_a → 0の極限では式(2)は式(1)に漸近する。\(\lim_{d_\mathrm{a} \rightarrow 0} Z_\mathrm{surf}\)
また，垂直入射吸音率は表面インピーダンスを用いて以下のように表せる。
・・・(複素音圧反射率)
・・・(垂直入射吸音率)
補足
-
複素音圧反射率は入射波振幅A, 反射波振幅Bの比の値として定義される。
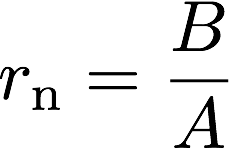
また，図.1に示すように，座標原点を材料表面に設定する時，表面インピーダンスは以下のように書ける。
上の２式よりA, Bを消去すると表面インピーダンスと複素音圧反射率の関係が導かれます。
多孔質材の内部流体モデル
多孔質材の内部流体モデルとしてよく用いられるものとして以下の3つのモデルがある。
・Miki model (\(\sigma, \phi, \alpha_\infty\))
円筒管内部音場の等価回路を基に，種々の多孔質材の実測値から構築された経験モデルである。
-
Miki modelは流れ抵抗率，空隙率，迷路度により以下の表される。（文献[1,2]を基に一部修正）
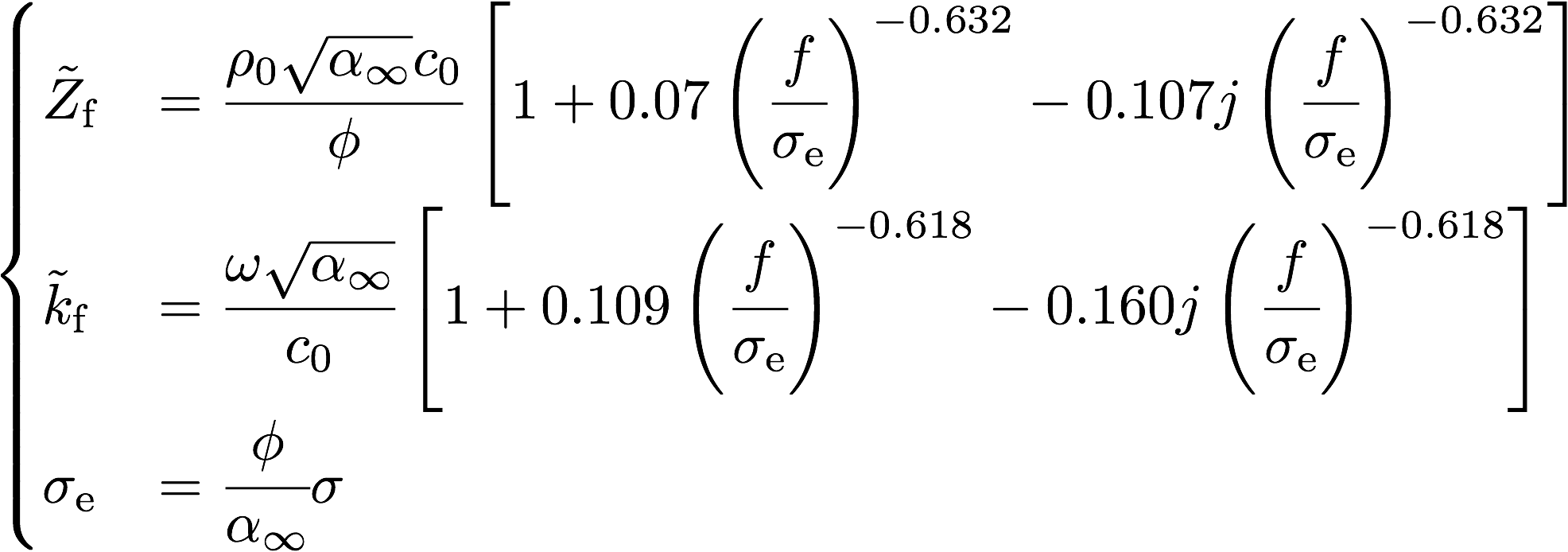
空隙率，迷路度ともに1.0とおいた式が使われることも多い。 詳細
文献
[1] Miki Y., Acoustical properties of porous materials - Modifications of Delany-Bazley models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 19-24[2] Miki Y., Acoustical properties of porous materials - Generalization of empirical models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 25-28
・Johnson-Champoux-Allard model (\(\sigma, \phi, \alpha_\infty, \Lambda, \Lambda^\prime\))
複素体積弾性率，実効密度の実測値における低音域，高音域の漸近挙動から構築された半現象論モデルである。
-
Johnson-Champoux-Allard modelは流れ抵抗率，空隙率，迷路度，粘性特性長，熱的特性長により以下の表される。
詳細
文献
[1] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402[2] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979
・Kato model (\(\rho_\mathrm{s}, \rho_\mathrm{b}, D\))
円筒管モデルを基に，ベッセル関数部の近似，実験に基づくパラメータ推定式・減衰に関する補正項を加えた半経験モデルである。
-
Kato modelにおいて，複素体積弾性率及び実効密度は以下のように与えられる。
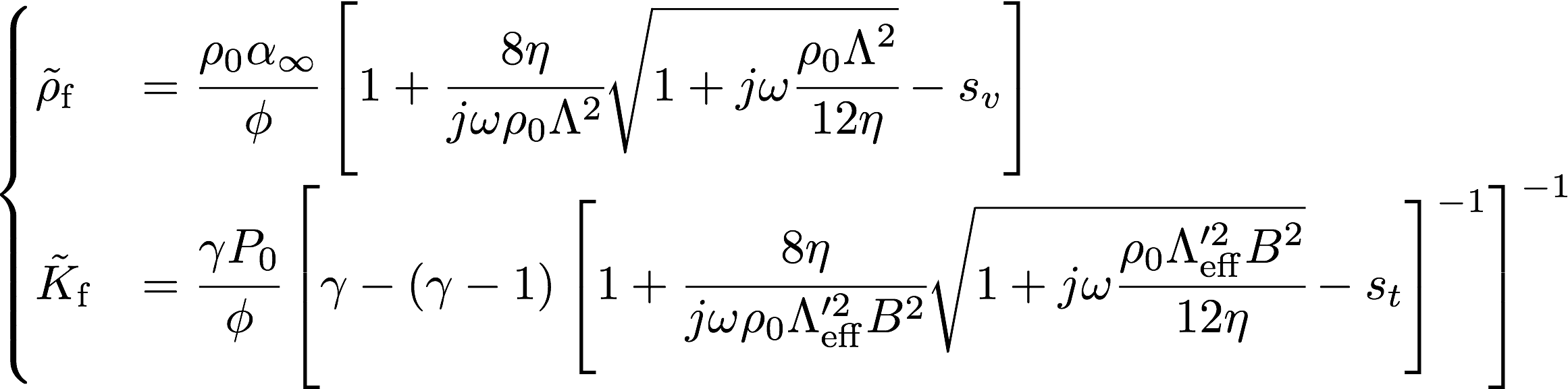
上式において，\(\Lambda, \Lambda^\prime_\mathrm{eff}, \alpha_\infty, s_\mathrm{v}, s_\mathrm{t}\)は以下のように与えられる。
熱的特性長はその定義から，物質密度 \(\rho_\mathrm{s}\)，嵩密度 \(\rho_\mathrm{b}\)，繊維径 \(D\)より理論的に算出することができる。
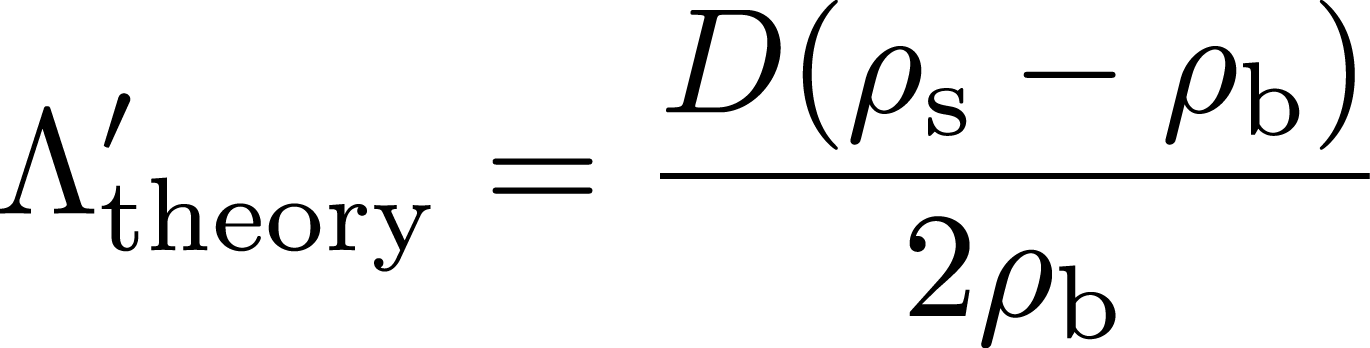
しかし，実際には繊維同士が接触することで，細孔内の表面積が減少する。この影響を考慮し，以下の実効的な熱的特性長を用いる。
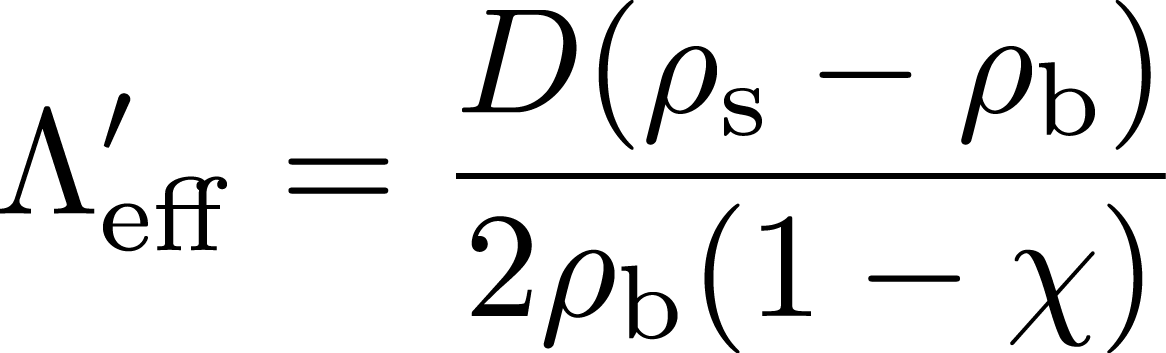
尚，接触率χについては以下の実験式を提案している。
円形断面繊維材料において繊維方向に対し垂直に音波が伝搬する場合に，熱的特性長と粘性特性長は以下の関係で表される[]。
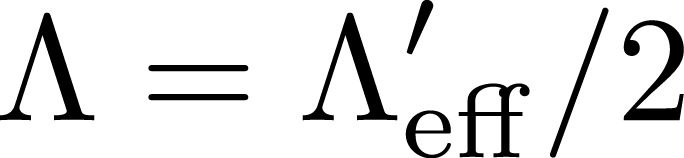
また，迷路度についても以下の実験式を提案している[]。
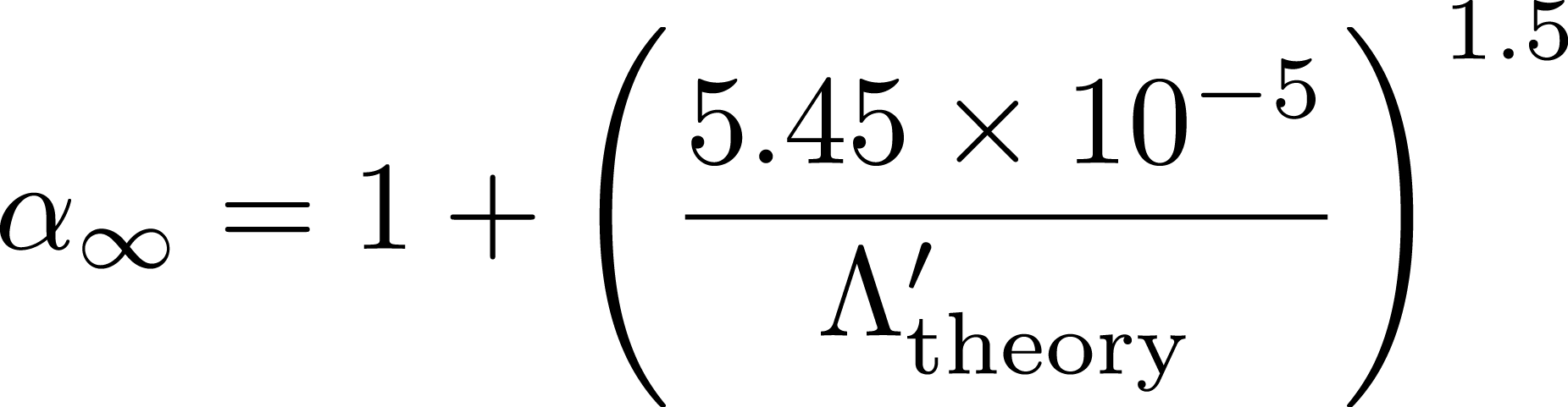
補正項にs_v,s_t についても以下の実験式を示している。
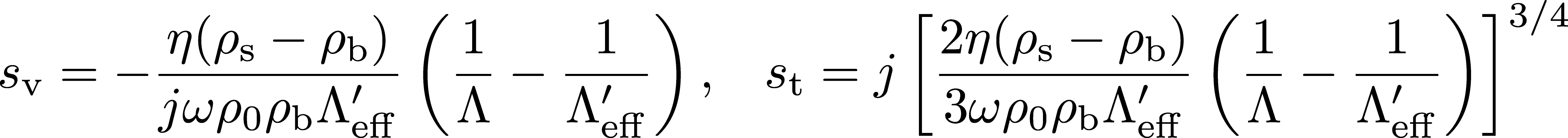
文献
[1] 加藤大輔 (2007) 多孔質材料内伝搬音の予測モデル -繊維不織布の物質密度と繊維径による定量化-. 日本音響学会誌 63 (11), 635-645.[2] 加藤大輔 (2008) 多孔質材料内伝搬音の予測モデル -Kato モデルにおける適用範囲の拡張-. 日本音響 学会誌 64 (6), 339-347.
特性インピーダンス，複素波数，複素体積弾性率，実効密度は以下の関係であらわされる。
