室内音響指標ベンチマーク

基本問題 A-21

残響時間が3秒程度の室で音声伝達性能を調べるためにSTIの計測を試みた。
受音点における（暗騒音を含む）音声レベル，暗騒音レベル，インパルス応答が以下の場合，STIを算出せよ。

レベル測定結果

周波数 (Hz)	125	250	500	1k	2k	4k	8k
音声レベル (dB)（暗騒音を含む）	50	45	42	40	36	36	30
暗騒音レベル (dB)	48	40	34	30	27	25	23

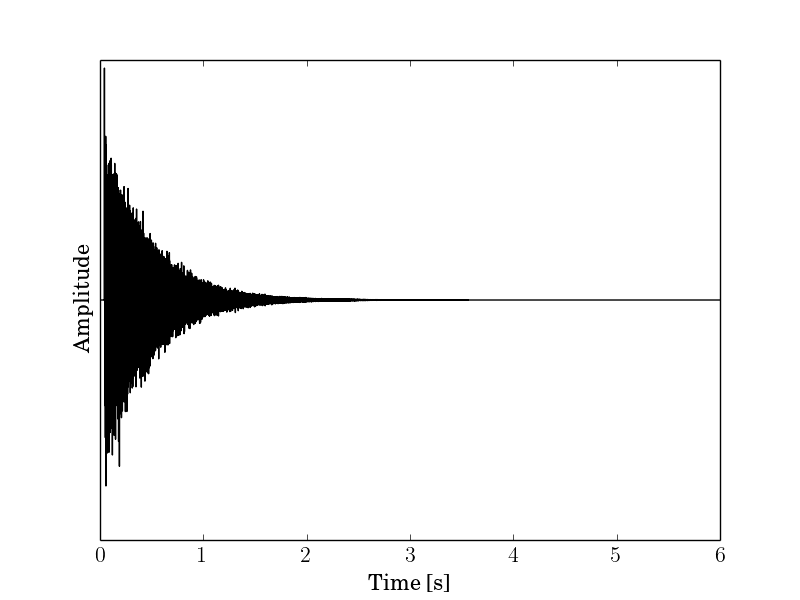
インパルス応答

a21.wav (RIFF waveform, 16 bit signed integer, モノラル, サンプリング周波数: 48000 Hz)
a21.fb (Float Binary (little endian), データ数 288000，モノラル，サンプリング周波数: 48000 Hz)
a21_wf

Note

　この応答はホワイトノイズを基に加工し，直接音を加えたものである。残響時間が3.0秒程度になるように時間的に指数減衰させている。

STI

	STI
Hoshi	0.311
Okubo	0.311
Nishikawa	0.310

算出プロセス（IEC 60268-16:2020 に準拠）

Step		変調周波数 $f_m$ (Hz)	周波数 $f_k$ (Hz)							備考
Step		変調周波数 $f_m$ (Hz)	125	250	500	1k	2k	4k	8k	備考
1	暗騒音を含んだ信号レベル　 $L_k$ [dB]		50	45	42	40	36	36	30	現場で，スピーカからTable A.4にある男性音声の特性を持つノイズを再生し，オクターブバンドごとに音圧レベル $\small{L_k}$ を計測し,右に記入する。
2	暗騒音レベル　 $L_{N,k}$ [dB]		48	40	34	30	27	25	23	現場で受音点の暗騒音レベルを計測し，右に記入する。
3	インパルス応答から計算したMTF　 $m_{k,\,f_m}$	0.63	0.740 27	0.769 69	0.739 96	0.759 97	0.753 84	0.751 73	0.753 63	インパルス応答 $\small{h(t)}$ からオクターブバンドに帯域制限した $\small{h_k(t)}$ を求め， $\small{h_k(t)}$ と変調周波数 $\small{f_m}$ からMTFを求める。 $m_{k,\,f_m} = \frac{\left\| \int \limits^{\infty}_{0} h^\textsf{2}_k (t)\,\exp (-j\textsf{2} \pi f_m t)\,\textsf{d}t \right\|}{\int\limits^{\infty}_{\textsf{0}}h^\textsf{2}_k (t)\,\textsf{d}t}$
		0.8	0.649 91	0.701 47	0.657 47	0.677 72	0.668 55	0.666 46	0.668 51
		1	0.554 66	0.636 95	0.581 28	0.593 66	0.581 66	0.579 71	0.581 63
		1.25	0.450 60	0.569 15	0.509 04	0.505 57	0.494 25	0.492 40	0.494 15
		1.6	0.331 51	0.481 24	0.430 48	0.407 63	0.403 94	0.401 15	0.401 66
		2	0.233 67	0.406 14	0.367 23	0.330 94	0.328 78	0.325 23	0.322 96
		2.5	0.183 20	0.372 73	0.297 01	0.291 37	0.262 58	0.256 78	0.257 49
		3.15	0.240 33	0.324 77	0.211 53	0.267 65	0.221 48	0.207 55	0.209 94
		4	0.341 37	0.198 10	0.148 52	0.211 24	0.196 06	0.177 05	0.166 66
		5	0.231 80	0.146 68	0.160 35	0.142 61	0.129 32	0.162 84	0.122 63
		5.3	0.091 27	0.189 23	0.116 21	0.086 68	0.114 87	0.122 70	0.114 22
		8	0.212 17	0.047 49	0.126 61	0.066 18	0.074 76	0.084 11	0.091 23
		10	0.120 39	0.064 71	0.090 82	0.065 88	0.096 62	0.036 43	0.083 29
		12.5	0.109 09	0.028 97	0.124 29	0.040 61	0.057 96	0.033 33	0.034 64
4	信号レベル　 $L_{S,k}$ [dB]		45.670 77	43.349 11	41.250 60	39.542 43	35.415 65	35.640 55	29.033 47	$\small{L_k}$ と $\small{L_{N,k}}$ から $\small{L_{S,k}}$ を求める。 $L_{S,k} = \textsf{10} \log _{\textsf{10}}\left[\textsf{10}^{(L_{k}/\textsf{10})}- \textsf{10}^{(L_{N,k}/\textsf{10})}\right]$
5	信号のSN比　 $\rho_k$ [dB]		-2.329 23	3.349 11	7.250 60	9.542 43	8.415 65	10.640 55	6.033 47	$\rho_k = L_{S,k} - L_{N,k}$
6	暗騒音の影響		0.369 04	0.683 77	0.841 51	0.900 00	0.874 11	0.920 57	0.800 47	$\left[ \textsf{1}+\textsf{10}^{-\rho_k /\textsf{10}} \right]^{-\textsf{1}} = \frac{I_{S,k}}{I_{S,k}+I_{N,k}} = \frac{I_{S,k}}{I_{k}}$
7	暗騒音の影響を含んだMTF　 $m^{\prime}_{k,\,f_m}$	0.63	0.273 19	0.526 29	0.622 68	0.683 97	0.658 93	0.692 02	0.603 26	$\begin{align} m^{\prime}_{k,\,f_m} &= m_{k,\,f_m} \cdot\left[ \textsf{1}+\textsf{10}^{-\rho_k /\textsf{10}} \right]^{-\textsf{1}} \\ &= m_{k,\,f_m} \times \frac{I_{S,k}}{I_{S,k}+I_{N,k}} \end{align}$
		0.8	0.239 84	0.479 65	0.553 26	0.609 95	0.584 38	0.613 53	0.535 13
		1	0.204 69	0.435 53	0.489 16	0.534 29	0.508 43	0.533 67	0.465 58
		1.25	0.166 29	0.389 17	0.428 37	0.455 01	0.432 02	0.453 29	0.395 55
		1.6	0.122 34	0.329 06	0.362 25	0.366 86	0.353 09	0.369 29	0.321 52
		2	0.086 23	0.277 70	0.309 03	0.297 84	0.287 39	0.299 39	0.258 52
		2.5	0.067 61	0.254 86	0.249 94	0.262 23	0.229 52	0.236 38	0.206 11
		3.15	0.088 69	0.222 07	0.178 00	0.240 88	0.193 60	0.191 07	0.168 05
		4	0.125 98	0.135 46	0.124 99	0.190 11	0.171 37	0.162 99	0.133 40
		5	0.085 54	0.100 30	0.134 94	0.128 35	0.113 04	0.149 90	0.098 17
		5.3	0.033 68	0.129 39	0.097 79	0.078 01	0.100 41	0.112 95	0.091 43
		8	0.078 30	0.032 48	0.106 54	0.059 56	0.065 35	0.077 43	0.073 03
		10	0.044 43	0.044 25	0.076 43	0.059 29	0.084 46	0.033 54	0.066 67
		12.5	0.040 26	0.019 81	0.104 59	0.036 55	0.050 66	0.030 69	0.027 73
8	暗騒音を含んだ信号の強度 $I_k$		100 000	31 623	15 849	10 000	3 981	3 981	1 000	$I_k = \textsf{10}^{(L_k/\textsf{10})}$
9	マスキングレベル $L_{a,k}$ [dB]		-	-40	-42.5	-44	-45	-47	-47	Table A.3 より演算する。125 Hzは算出しない。
10	マスキングの強度　 $a_k$		-	0.000 10	0.000 06	0.000 04	0.000 03	0.000 02	0.000 02	125 Hzは算出しない。 $a_{k} = \textsf{10}^{(L_{a,k}/\textsf{10})}$
11	マスキングを考慮した音声の強度 $I_{am,k}$		0	10	1.7782794	0.6309573	0.3162278	0.079	0.0794	125 Hzは 0 とする。 $I_{am,k} = a_k \times I_{k-\textsf{1}}$
	最小可聴値 $A_k$ [dB]		46	27	12	6.5	7.5	8	12	Table A.2で与えられている値を用いる。
12	最小可聴値の強度　 $I_{\textsf{rt},k}$		39810.72	501.19	15.85	4.47	5.62	6.31	15.85	$I_{\textsf{rt},k} = \textsf{10}^{(A_k/\textsf{10})}$
13	聴覚マスキングの影響　 $C_k$		0.715 25	0.984 09	0.998 89	0.999 49	0.998 51	0.998 40	0.984 32	$C_k = \frac{I_k}{I_k+I_{am,k}+I_{\textsf{rt},k}}$
14	マスキングを考慮したMTF　 $m^{\prime\prime}_{k,\,f_m}$	0.63	0.195 40	0.517 92	0.621 99	0.683 62	0.657 95	0.690 91	0.593 80	$m^{\prime\prime}_{k,\,f_m} = m^{\prime}_{k,\,f_m} \times C_k$
		0.8	0.171 55	0.472 02	0.552 65	0.609 64	0.583 51	0.612 54	0.526 74
		1	0.146 41	0.428 60	0.488 61	0.534 02	0.507 67	0.532 81	0.458 28
		1.25	0.118 94	0.382 98	0.427 89	0.454 78	0.431 38	0.452 56	0.389 35
		1.6	0.087 51	0.323 83	0.361 85	0.366 68	0.352 56	0.368 70	0.316 48
		2	0.061 68	0.273 29	0.308 68	0.297 69	0.286 96	0.298 91	0.254 46
		2.5	0.048 36	0.250 81	0.249 66	0.262 10	0.229 18	0.236 00	0.202 88
		3.15	0.063 44	0.218 53	0.177 80	0.240 76	0.193 31	0.190 76	0.165 41
		4	0.090 11	0.133 30	0.124 85	0.190 02	0.171 12	0.162 72	0.131 31
		5	0.061 19	0.098 70	0.134 79	0.128 28	0.112 87	0.149 66	0.096 63
		5.3	0.024 09	0.127 33	0.097 68	0.077 97	0.100 26	0.112 77	0.090 00
		8	0.056 01	0.031 96	0.106 42	0.059 53	0.065 25	0.077 31	0.071 89
		10	0.031 78	0.043 54	0.076 34	0.059 26	0.084 33	0.033 48	0.065 62
		12.5	0.028 80	0.019 49	0.104 48	0.036 53	0.050 59	0.030 64	0.027 30
15	等価SN比に換算　 $\rho_{\textsf{eff}_ {k,\,f_m}}$ [dB]	0.63	-6.146 51	0.311 42	2.162 84	3.346 15	2.841 09	3.493 36	1.649 09	-15 ≤ $\small{\rho_{\textsf{eff}_{k,\,f_m}}}$ ≤ +15 に収める。 $\rho_{\textbf{eff}\,_{k,\,f_m}}=\textsf{10} \log_{\textsf{10}}\left( \frac{m^{\prime\prime}_{k,\,f_m}}{\textsf{1}-m^{\prime\prime}_{k,\,f_m}} \right)$
		0.8	-6.838 78	-0.486 63	0.918 02	1.936 05	1.464 48	1.989 12	0.464 92
		1	-7.656 90	-1.248 87	-0.197 85	0.591 87	0.133 34	0.570 79	-0.726 45
		1.25	-8.696 77	-2.071 22	-1.261 49	-0.787 69	-1.199 61	-0.826 62	-1.954 46
		1.6	-10.181 91	-3.197 45	-2.463 93	-2.373 41	-2.639 61	-2.335 72	-3.344 05
		2	-11.822 13	-4.247 45	-3.501 66	-3.727 60	-3.952 95	-3.702 28	-4.668 41
		2.5	-12.940 00	-4.752 56	-4.779 10	-4.495 32	-5.267 73	-5.101 77	-5.942 77
		3.15	-11.691 94	-5.533 93	-6.650 35	-4.987 91	-6.204 59	-6.275 85	-7.028 97
		4	-10.042 29	-8.130 37	-8.457 09	-6.296 82	-6.851 96	-7.114 16	-8.205 58
		5	-11.859 29	-9.605 54	-8.074 76	-8.322 18	-8.954 03	-7.544 72	-9.707 73
		5.3	-15.000 00	-8.359 17	-9.655 54	-10.728 26	-9.529 94	-8.958 32	-10.047 96
		8	-12.267 42	-14.813 04	-9.241 03	-11.986 06	-11.560 80	-10.768 50	-11.109 56
		10	-14.838 43	-13.417 29	-10.827 40	-12.007 29	-10.357 49	-14.603 61	-11.534 70
		12.5	-15.000 00	-15.000 00	-9.330 52	-14.211 39	-12.733 99	-15.000 00	-15.000 00
16	$TI$ を算出　 $TI_{k,\,f_m}$	0.63	0.295 12	0.510 38	0.572 09	0.611 54	0.594 70	0.616 45	0.554 97	0 ≤ TI ≤ +1 であることを確認する $TI_{k,\,f_m} = \frac{\rho_{\textbf{eff}\,_{k,\,f_m}}+\textsf{15}}{\textsf{30}}$
		0.8	0.272 04	0.483 78	0.530 60	0.564 53	0.548 82	0.566 30	0.515 50
		1	0.244 77	0.458 37	0.493 40	0.519 73	0.504 44	0.519 03	0.475 78
		1.25	0.210 11	0.430 96	0.457 95	0.473 74	0.460 01	0.472 45	0.434 85
		1.6	0.160 60	0.393 42	0.417 87	0.420 89	0.412 01	0.422 14	0.388 53
		2	0.105 93	0.358 42	0.383 28	0.375 75	0.368 23	0.376 59	0.344 39
		2.5	0.068 67	0.341 58	0.340 70	0.350 16	0.324 41	0.329 94	0.301 91
		3.15	0.110 27	0.315 54	0.278 32	0.333 74	0.293 18	0.290 80	0.265 70
		4	0.165 26	0.228 99	0.218 10	0.290 11	0.271 60	0.262 86	0.226 48
		5	0.104 69	0.179 82	0.230 84	0.222 59	0.201 53	0.248 51	0.176 41
		5.3	0.000 00	0.221 36	0.178 15	0.142 39	0.182 34	0.201 39	0.165 07
		8	0.091 09	0.006 23	0.191 97	0.100 46	0.114 64	0.141 05	0.129 68
		10	0.005 39	0.052 76	0.139 09	0.099 76	0.154 75	0.013 21	0.115 51
		12.5	0.000 00	0.000 00	0.188 98	0.026 29	0.075 53	0.000 00	0.000 00
17	$MTI_k$ を算出		0.130 99	0.284 40	0.330 10	0.323 69	0.321 87	0.318 62	0.292 48	$MTI_k = \frac{\textsf{1}}{\textsf{14}}\sum^{\textsf{14}}_{m=\textsf{1}}TI_{k,\,f_m}$
	男性の音声スペクトルによる重み付け	α	0.085	0.127	0.230	0.233	0.309	0.224	0.173	Table A.1 で与えられている値を利用する。
	男性の音声スペクトルによる重み付け	β	0.085	0.078	0.065	0.011	0.047	0.095	-	Table A.1 で与えられている値を利用する。
18	STI		0.311					$STI = \sum^\textsf{7}_{k=\textsf{1}}\alpha_k \times MTI_k - \sum^\textsf{6}_{k=\textsf{1}}\beta_k \times \sqrt{MTI_k \times MTI_{k+\textsf{1}}}$

Table A.1 -- MTI 重み付け係数

中心周波数 [Hz]		125	250	500	1k	2k	4k	8k
男性	α	0.085	0.127	0.230	0.233	0.309	0.224	0.173
男性	β	0.085	0.078	0.065	0.011	0.047	0.095	-

Table A.2 -- 聴覚マスキングレベル

$\small{(k-1)}$ 番目の中心周波数の音声レベル $\small{L_{k-1}}$ [dB]	< 63	≥ 63 かつ < 67	≥ 67 かつ < 100	≥ 100
$\small{k}$ 番目の中心周波数のマスキングレベル $\small{L_{a,\,k}}$ [dB]	$\scriptsize{0.5 \times L_{k-1} -65.0}$	$\scriptsize{1.8 \times L_{k-1} -146.9}$	$\scriptsize{0.5 × L_{k-1} -59.8}$	$\scriptsize{-10}$

Table A.3 -- 最小可聴値（最小検知限）

中心周波数 [Hz]	125	250	500	1k	2k	4k	8k
最小可聴値 $\small{A_k}$ [dB]	46	27	12	6.5	7.5	8	12

Table A.4 -- 男性音声のスペクトル

中心周波数 [Hz]	125	250	500	1k	2k	4k	8k	A特性
男性音声の相対レベル [dB]	-2.5	0.5	0	-6	-12	-18	-24	0.0