確認問題 B-31
残響時間が0.5秒程度の室で音声伝達性能を調べるためにSTIの計測を試みた。
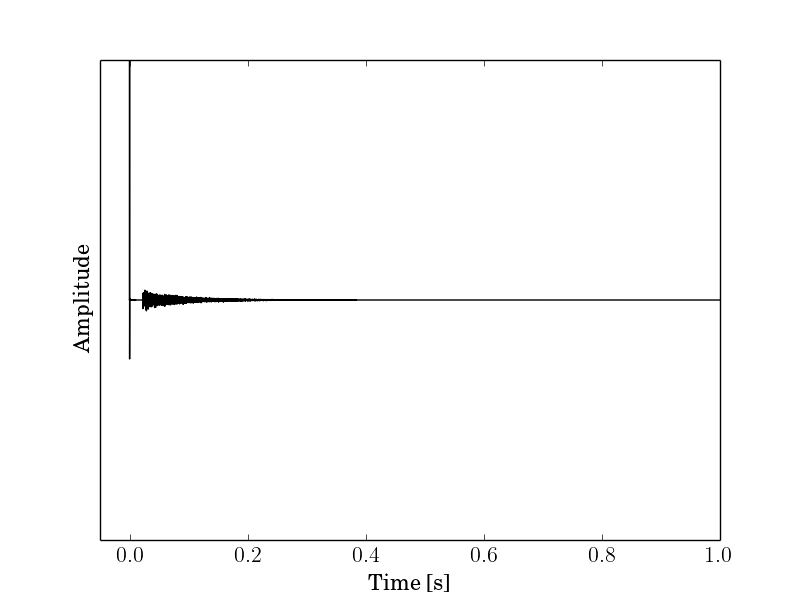
受音点における(暗騒音を含む)音声レベル,暗騒音レベル,インパルス応答が以下の場合,STIを算出せよ。
レベル測定結果
| 周波数 (Hz) | 125 | 250 | 500 | 1k | 2k | 4k | 8k |
| 音声レベル (dB)(暗騒音含む) | 67 | 67 | 64 | 58 | 52 | 46 | 40 |
| 暗騒音レベル (dB) | 48 | 40 | 34 | 30 | 27 | 25 | 23 |
インパルス応答
b31.wav (RIFF waveform, 16 bit signed integer, モノラル, サンプリング周波数: 48000 Hz)b31.fb (Float Binary (little endian), データ数 288000,モノラル,サンプリング周波数: 48000 Hz)
Note
この応答はホワイトノイズを基に加工し,ファイルの先頭に直接音を加えたものである。残響時間が0.5秒程度になるように時間的に指数減衰させている。インパルス応答をフィルタリングするときに,直接音がデータの後ろに回り込まないように注意しよう。また TI が 0 から 1 の間の値になるように注意しよう。STI
| STI | |
| Hoshi | 0.902 |
| Nishikawa | 0.902 |
| Okubo | 0.902 |
算出プロセス(IEC 60268-16:2020 に準拠)
| Step | 変調 周波数 $f_m$ (Hz) |
周波数 $f_k$ (Hz) | 備考 | |||||||
| 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | ||||
| 1 | 暗騒音を含んだ信号レベル $L_k$ [dB] | 67 | 67 | 64 | 58 | 52 | 46 | 40 | 現場で,スピーカからTable A.4にある男性音声の特性を持つノイズを再生し,受音点でオクターブバンドごとに音圧レベル $\small{L_k}$ を計測し,右に記入する。 | |
| 2 | 暗騒音レベル $L_{N,k}$ [dB] | 48 | 40 | 34 | 30 | 27 | 25 | 23 | 現場で受音点の暗騒音レベルを計測し,右に記入する。 | |
| 3 | インパルス応答から計算したMTF $m_{k,\,f_m}$ | 0.63 | 0.997 69 | 0.996 51 | 0.997 12 | 0.997 02 | 0.997 30 | 0.997 17 | 0.994 28 | インパルス応答 $\small{h(t)}$ からオクターブバンドに帯域制限した $\small{h_k(t)}$ を求め,$\small{h_k(t)}$ と変調周波数 $\small{f_m}$ からMTFを求める。 \[ m_{k,\,f_m} = \frac{\left| \int \limits^{\infty}_{0} h^\textsf{2}_k (t)\,\exp (-j\textsf{2} \pi f_m t)\,\textsf{d}t \right|}{\int\limits^{\infty}_{\textsf{0}}h^\textsf{2}_k (t)\,\textsf{d}t} \] |
| 0.8 | 0.996 31 | 0.994 44 | 0.995 40 | 0.995 26 | 0.995 69 | 0.995 49 | 0.990 88 | |||
| 1 | 0.994 32 | 0.991 44 | 0.992 94 | 0.992 71 | 0.993 39 | 0.993 07 | 0.985 99 | |||
| 1.25 | 0.991 34 | 0.986 94 | 0.989 25 | 0.988 90 | 0.989 94 | 0.989 45 | 0.978 65 | |||
| 1.6 | 0.986 38 | 0.979 45 | 0.983 15 | 0.982 61 | 0.984 25 | 0.983 49 | 0.966 50 | |||
| 2 | 0.979 83 | 0.969 66 | 0.975 24 | 0.974 43 | 0.976 88 | 0.975 75 | 0.950 66 | |||
| 2.5 | 0.970 78 | 0.956 39 | 0.964 61 | 0.963 46 | 0.967 01 | 0.965 36 | 0.929 27 | |||
| 3.15 | 0.958 28 | 0.938 96 | 0.950 71 | 0.949 20 | 0.954 16 | 0.951 77 | 0.901 09 | |||
| 4 | 0.941 77 | 0.918 28 | 0.933 92 | 0.932 52 | 0.938 89 | 0.935 40 | 0.866 92 | |||
| 5 | 0.923 57 | 0.899 27 | 0.917 20 | 0.917 52 | 0.924 39 | 0.919 53 | 0.833 30 | |||
| 5.3 | 0.903 34 | 0.884 22 | 0.900 28 | 0.905 59 | 0.911 23 | 0.905 03 | 0.800 53 | |||
| 8 | 0.882 69 | 0.878 28 | 0.885 35 | 0.898 58 | 0.901 35 | 0.895 21 | 0.773 08 | |||
| 10 | 0.868 97 | 0.877 88 | 0.877 15 | 0.895 38 | 0.897 01 | 0.891 48 | 0.759 21 | |||
| 12.5 | 0.868 75 | 0.866 70 | 0.878 97 | 0.894 79 | 0.900 34 | 0.890 17 | 0.758 89 | |||
| 4 | 信号レベル $L_{S,k}$ [dB] | 66.944 98 | 66.991 33 | 63.995 65 | 57.993 11 | 51.986 24 | 45.965 37 | 39.912 47 | $\small{L_k}$ と $\small{L_{N,k}}$ から $\small{L_{S,k}}$ を求める。 \[ L_{S,k} = \textsf{10} \log _{\textsf{10}}\left[\textsf{10}^{(L_{k}/\textsf{10})}- \textsf{10}^{(L_{N,k}/\textsf{10})}\right] \] | |
| 5 | 信号のSN比 $\rho_k$ [dB] | 18.944 98 | 26.991 33 | 29.995 65 | 27.993 11 | 24.986 24 | 20.965 37 | 16.912 47 | \[ \rho_k = L_{S,k} - L_{N,k} \] | |
| 6 | 暗騒音の影響 | 0.987 41 | 0.998 00 | 0.999 00 | 0.998 42 | 0.996 84 | 0.992 06 | 0.980 05 | \[ \left[ \textsf{1}+\textsf{10}^{-\rho_k /\textsf{10}} \right]^{-\textsf{1}} = \frac{I_{S,k}}{I_{S,k}+I_{N,k}} = \frac{I_{S,k}}{I_{k}} \] | |
| 7 | 暗騒音の影響を含んだMTF $m^{\prime}_{k,\,f_m}$ | 0.63 | 0.985 13 | 0.994 52 | 0.996 12 | 0.995 44 | 0.994 14 | 0.989 25 | 0.974 44 | \begin{align*} m^{\prime}_{k,\,f_m} &= m_{k,\,f_m} \cdot\left[ \textsf{1}+\textsf{10}^{-\rho_k /\textsf{10}} \right]^{-\textsf{1}} \\ &= m_{k,\,f_m} \times \frac{I_{S,k}}{I_{S,k}+I_{N,k}} \end{align*} |
| 0.8 | 0.983 77 | 0.992 45 | 0.994 41 | 0.993 68 | 0.992 55 | 0.987 58 | 0.971 11 | |||
| 1 | 0.981 81 | 0.989 46 | 0.991 94 | 0.991 14 | 0.990 25 | 0.985 18 | 0.966 31 | |||
| 1.25 | 0.978 86 | 0.984 97 | 0.988 26 | 0.987 34 | 0.986 81 | 0.981 59 | 0.959 12 | |||
| 1.6 | 0.973 96 | 0.977 50 | 0.982 17 | 0.981 05 | 0.981 14 | 0.975 67 | 0.947 21 | |||
| 2 | 0.967 50 | 0.967 72 | 0.974 27 | 0.972 89 | 0.973 79 | 0.968 00 | 0.931 69 | |||
| 2.5 | 0.958 56 | 0.954 48 | 0.963 65 | 0.961 93 | 0.963 95 | 0.957 69 | 0.910 73 | |||
| 3.15 | 0.946 22 | 0.937 09 | 0.949 76 | 0.947 70 | 0.951 14 | 0.944 21 | 0.883 11 | |||
| 4 | 0.929 91 | 0.916 45 | 0.932 99 | 0.931 05 | 0.935 92 | 0.927 97 | 0.849 63 | |||
| 5 | 0.911 95 | 0.897 48 | 0.916 29 | 0.916 06 | 0.921 47 | 0.912 22 | 0.816 67 | |||
| 5.3 | 0.891 97 | 0.882 46 | 0.899 38 | 0.904 15 | 0.908 35 | 0.897 84 | 0.784 55 | |||
| 8 | 0.871 58 | 0.876 53 | 0.884 46 | 0.897 16 | 0.898 50 | 0.888 10 | 0.757 65 | |||
| 10 | 0.858 03 | 0.876 13 | 0.876 28 | 0.893 97 | 0.894 18 | 0.884 40 | 0.744 06 | |||
| 12.5 | 0.857 82 | 0.864 97 | 0.878 09 | 0.893 38 | 0.897 49 | 0.883 10 | 0.743 74 | |||
| 8 | 暗騒音を含んだ信号の強度 $I_k$ | 5 011 872 | 5 011 872 | 2 511 886 | 630 957 | 158 489 | 39 811 | 10 000 | \[ I_k = \textsf{10}^{(L_k/\textsf{10})} \] | |
| 9 | マスキングレベル $L_{a,k}$ [dB] | - | -26.3 | -26.3 | -31.7 | -36 | -39 | -42 | Table A.3 より演算する。125 Hzは算出しない。 | |
| 10 | マスキングの強度 $a_k$ | - | 0.002 34 | 0.002 34 | 0.000 68 | 0.000 25 | 0.000 13 | 0.000 06 | 125 Hzは算出しない。 \[ a_{k} = \textsf{10}^{(L_{a,k}/\textsf{10})} \] | |
| 11 | マスキングを考慮した音声の強度 $I_{am,k}$ | 0 | 11748.976 | 11748.976 | 1698.2437 | 158.48932 | 19.953 | 2.5119 | 125 Hzは 0 とする。 \[ I_{am,k} = a_k \times I_{k-\textsf{1}} \] | |
| 最小可聴値 $A_k$ [dB] | 46 | 27 | 12 | 6.5 | 7.5 | 8 | 12 | Table A.2で与えられている値を用いる。 | ||
| 12 | 最小可聴値の強度 $I_{\textsf{rt},k}$ | 39810.72 | 501.19 | 15.85 | 4.47 | 5.62 | 6.31 | 15.85 | \[ I_{\textsf{rt},k} = \textsf{10}^{(A_k/\textsf{10})} \] | |
| 13 | 聴覚マスキングの影響 $C_k$ | 0.992 12 | 0.997 56 | 0.995 34 | 0.997 31 | 0.998 97 | 0.999 34 | 0.998 17 | \[ C_k = \frac{I_k}{I_k+I_{am,k}+I_{\textsf{rt},k}} \] | |
| 14 | マスキングを考慮したMTF $m^{\prime\prime}_{k,\,f_m}$ | 0.63 | 0.977 36 | 0.992 10 | 0.991 47 | 0.992 76 | 0.993 12 | 0.988 59 | 0.972 65 | \[ m^{\prime\prime}_{k,\,f_m} = m^{\prime}_{k,\,f_m} \times C_k \] |
| 0.8 | 0.976 01 | 0.990 03 | 0.989 77 | 0.991 00 | 0.991 52 | 0.986 93 | 0.969 33 | |||
| 1 | 0.974 07 | 0.987 05 | 0.987 32 | 0.988 47 | 0.989 22 | 0.984 53 | 0.964 54 | |||
| 1.25 | 0.971 15 | 0.982 57 | 0.983 65 | 0.984 68 | 0.985 79 | 0.980 95 | 0.957 37 | |||
| 1.6 | 0.966 28 | 0.975 11 | 0.977 59 | 0.978 41 | 0.980 12 | 0.975 03 | 0.945 48 | |||
| 2 | 0.959 87 | 0.965 36 | 0.969 72 | 0.970 27 | 0.972 78 | 0.967 36 | 0.929 98 | |||
| 2.5 | 0.951 01 | 0.952 15 | 0.959 16 | 0.959 34 | 0.962 95 | 0.957 06 | 0.909 06 | |||
| 3.15 | 0.938 76 | 0.934 80 | 0.945 33 | 0.945 15 | 0.950 16 | 0.943 58 | 0.881 49 | |||
| 4 | 0.922 58 | 0.914 21 | 0.928 64 | 0.928 54 | 0.934 95 | 0.927 36 | 0.848 07 | |||
| 5 | 0.904 76 | 0.895 29 | 0.912 01 | 0.913 60 | 0.920 52 | 0.911 62 | 0.815 18 | |||
| 5.3 | 0.884 94 | 0.880 30 | 0.895 19 | 0.901 72 | 0.907 41 | 0.897 25 | 0.783 12 | |||
| 8 | 0.864 71 | 0.874 39 | 0.880 34 | 0.894 75 | 0.897 57 | 0.887 52 | 0.756 27 | |||
| 10 | 0.851 27 | 0.874 00 | 0.872 19 | 0.891 56 | 0.893 25 | 0.883 82 | 0.742 70 | |||
| 12.5 | 0.851 06 | 0.862 86 | 0.874 00 | 0.890 97 | 0.896 56 | 0.882 52 | 0.742 38 | |||
| 15 | 等価SN比に換算 $\rho_{\textsf{eff}_ {k,\,f_m}}$ [dB] | 0.63 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | -15 ≤ $\small{\rho_{\textsf{eff}_{k,\,f_m}}}$ ≤ +15 に収める。 \[ \rho_{\textbf{eff}\,_{k,\,f_m}}=\textsf{10} \log_{\textsf{10}}\left( \frac{m^{\prime\prime}_{k,\,f_m}}{\textsf{1}-m^{\prime\prime}_{k,\,f_m}} \right) \] |
| 0.8 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 14.997 46 | |||
| 1 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 14.346 15 | |||
| 1.25 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 13.513 26 | |||
| 1.6 | 14.572 51 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 15.000 00 | 12.390 64 | |||
| 2 | 13.787 67 | 14.451 47 | 15.000 00 | 15.000 00 | 15.000 00 | 14.718 26 | 11.232 71 | |||
| 2.5 | 12.880 61 | 12.988 70 | 13.707 75 | 13.728 40 | 14.148 48 | 13.480 85 | 9.998 27 | |||
| 3.15 | 11.855 11 | 11.564 84 | 12.378 57 | 12.363 02 | 12.801 94 | 12.233 84 | 8.714 68 | |||
| 4 | 10.761 77 | 10.276 14 | 11.143 71 | 11.137 34 | 11.575 44 | 11.060 71 | 7.467 84 | |||
| 5 | 9.777 06 | 9.319 86 | 10.155 87 | 10.242 19 | 10.637 64 | 10.134 78 | 6.444 93 | |||
| 5.3 | 8.859 96 | 8.665 56 | 9.315 06 | 9.625 94 | 9.912 21 | 9.411 14 | 5.576 00 | |||
| 8 | 8.056 19 | 8.426 93 | 8.667 04 | 9.294 61 | 9.426 24 | 8.970 85 | 4.917 57 | |||
| 10 | 7.576 79 | 8.411 26 | 8.340 49 | 9.149 58 | 9.226 11 | 8.812 22 | 4.603 67 | |||
| 12.5 | 7.569 37 | 7.987 80 | 8.411 36 | 9.123 26 | 9.379 04 | 8.757 54 | 4.596 51 | |||
| 16 | $TI$ を算出 $TI_{k,\,f_m}$ | 0.63 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 0 ≤ TI ≤ +1 であることを確認する \[ TI_{k,\,f_m} = \frac{\rho_{\textbf{eff}\,_{k,\,f_m}}+\textsf{15}}{\textsf{30}} \] |
| 0.8 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 0.999 92 | |||
| 1 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 0.978 20 | |||
| 1.25 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 0.950 44 | |||
| 1.6 | 0.985 75 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 0.913 02 | |||
| 2 | 0.959 59 | 0.981 72 | 1.000 00 | 1.000 00 | 1.000 00 | 0.990 61 | 0.874 42 | |||
| 2.5 | 0.929 35 | 0.932 96 | 0.956 92 | 0.957 61 | 0.971 62 | 0.949 36 | 0.833 28 | |||
| 3.15 | 0.895 17 | 0.885 49 | 0.912 62 | 0.912 10 | 0.926 73 | 0.907 79 | 0.790 49 | |||
| 4 | 0.858 73 | 0.842 54 | 0.871 46 | 0.871 24 | 0.885 85 | 0.868 69 | 0.748 93 | |||
| 5 | 0.825 90 | 0.810 66 | 0.838 53 | 0.841 41 | 0.854 59 | 0.837 83 | 0.714 83 | |||
| 5.3 | 0.795 33 | 0.788 85 | 0.810 50 | 0.820 86 | 0.830 41 | 0.813 70 | 0.685 87 | |||
| 8 | 0.768 54 | 0.780 90 | 0.788 90 | 0.809 82 | 0.814 21 | 0.799 03 | 0.663 92 | |||
| 10 | 0.752 56 | 0.780 38 | 0.778 02 | 0.804 99 | 0.807 54 | 0.793 74 | 0.653 46 | |||
| 12.5 | 0.752 31 | 0.766 26 | 0.780 38 | 0.804 11 | 0.812 63 | 0.791 92 | 0.653 22 | |||
| 17 | $\small{MTI_k}$ を算出 | 0.894 52 | 0.897 84 | 0.909 81 | 0.915 87 | 0.921 68 | 0.910 91 | 0.818 57 | \[ MTI_k = \frac{\textsf{1}}{\textsf{14}}\sum^{\textsf{14}}_{m=\textsf{1}}TI_{k,\,f_m} \] | |
| 男性の音声スペクトルによる重み付け | α | 0.085 | 0.127 | 0.230 | 0.233 | 0.309 | 0.224 | 0.173 | Table A.1 で与えられている値を利用する。 | |
| β | 0.085 | 0.078 | 0.065 | 0.011 | 0.047 | 0.095 | - | |||
| 18 | STI | 0.902 | \[ STI = \sum^\textsf{7}_{k=\textsf{1}}\alpha_k \times MTI_k - \sum^\textsf{6}_{k=\textsf{1}}\beta_k \times \sqrt{MTI_k \times MTI_{k+\textsf{1}}} \] | |||||||
Table A.1 -- MTI 重み付け係数
| 中心周波数 [Hz] | 125 | 250 | 500 | 1k | 2k | 4k | 8k | |
| 男性 | α | 0.085 | 0.127 | 0.230 | 0.233 | 0.309 | 0.224 | 0.173 |
| β | 0.085 | 0.078 | 0.065 | 0.011 | 0.047 | 0.095 | - | |
Table A.2 -- 聴覚マスキングレベル
| $\small{(k-1)}$ 番目の中心周波数の音声レベル $\small{L_{k-1}}$ [dB] |
< 63 | ≥ 63 かつ < 67 | ≥ 67 かつ < 100 | ≥ 100 |
| $\small{k}$ 番目の中心周波数のマスキングレベル $\small{L_{a,\,k}}$ [dB] |
$\scriptsize{0.5 \times L_{k-1} -65.0}$ | $\scriptsize{1.8 \times L_{k-1} -146.9}$ | $\scriptsize{0.5 × L_{k-1} -59.8}$ | $\scriptsize{-10}$ |
Table A.3 -- 最小可聴値(最小検知限)
| 中心周波数 [Hz] | 125 | 250 | 500 | 1k | 2k | 4k | 8k |
| 最小可聴値 $\small{A_k}$ [dB] | 46 | 27 | 12 | 6.5 | 7.5 | 8 | 12 |
Table A.4 -- 男性音声のスペクトル
| 中心周波数 [Hz] | 125 | 250 | 500 | 1k | 2k | 4k | 8k | A特性 |
| 男性音声の 相対レベル [dB] |
-2.5 | 0.5 | 0 | -6 | -12 | -18 | -24 | 0.0 |