室内音響指標ベンチマーク

コラム５：音響指標の算出に用いるオクターブバンドフィルタの設計

はじめに

　音響指標の算出にオクターブバンドフィルタの設計は欠かせない。オクターブバンドおよび1/Nオクターブバンドフィルタに関する規定は，IEC 61260-1 および JIS C1514にあり，基本的にこれらに則り設計すればよい。しかしフィルタの設計は信号処理の範疇であるため，具体的なバンドパスフィルタの設計方法を紹介している建築音響の書籍はほとんどない。またそのためか，フィルタの設計が音響指標に与える影響を言及した書籍や文書もほとんどみあたらない。そこで本コラムでは，実際にFIRフィルタとIIRフィルタを使ってバンドパスフィルタ設計することで，設計上の注意点を洗い出すとともに，さらに音響指標のひとつであるC₈₀を算出し，音響指標への影響を探ることにした。

何が問題となるのか？

　まずはじめに窓関数法を用いてFIRによるバンドパスフィルタ設計した。使用した窓はHanning Windowである。フィルタ窓の大きさと周波数特性の関係をみてみよう。図1に125 Hz帯域オクターブバンドフィルタの周波数特性を，図2に1 kHz帯域オクターブバンドフィルタの周波数特性をそれぞれ示す。図中の黒線はIEC 61260-1 （またはJIS）に定義された class 1の上限値と下限値を表している。設計したバンドパスフィルタの周波数特性がこれらの間に収まればよい。 　まず図1をみると，窓の大きさ (Wn) は4096サンプル以上必要であることがわかる。一方図2をみると，窓の大きさは512サンプルでも十分であることがわかる。このように窓関数法でFIRフィルタを設計する場合，必要な窓の大きさと周波数（帯域）は反比例の関係にあるから，63 Hz帯域では8192サンプル，31.5 Hz帯域では16384サンプル必要であることは自明である。このことは低音域ほど波長が長いことからも理解できる。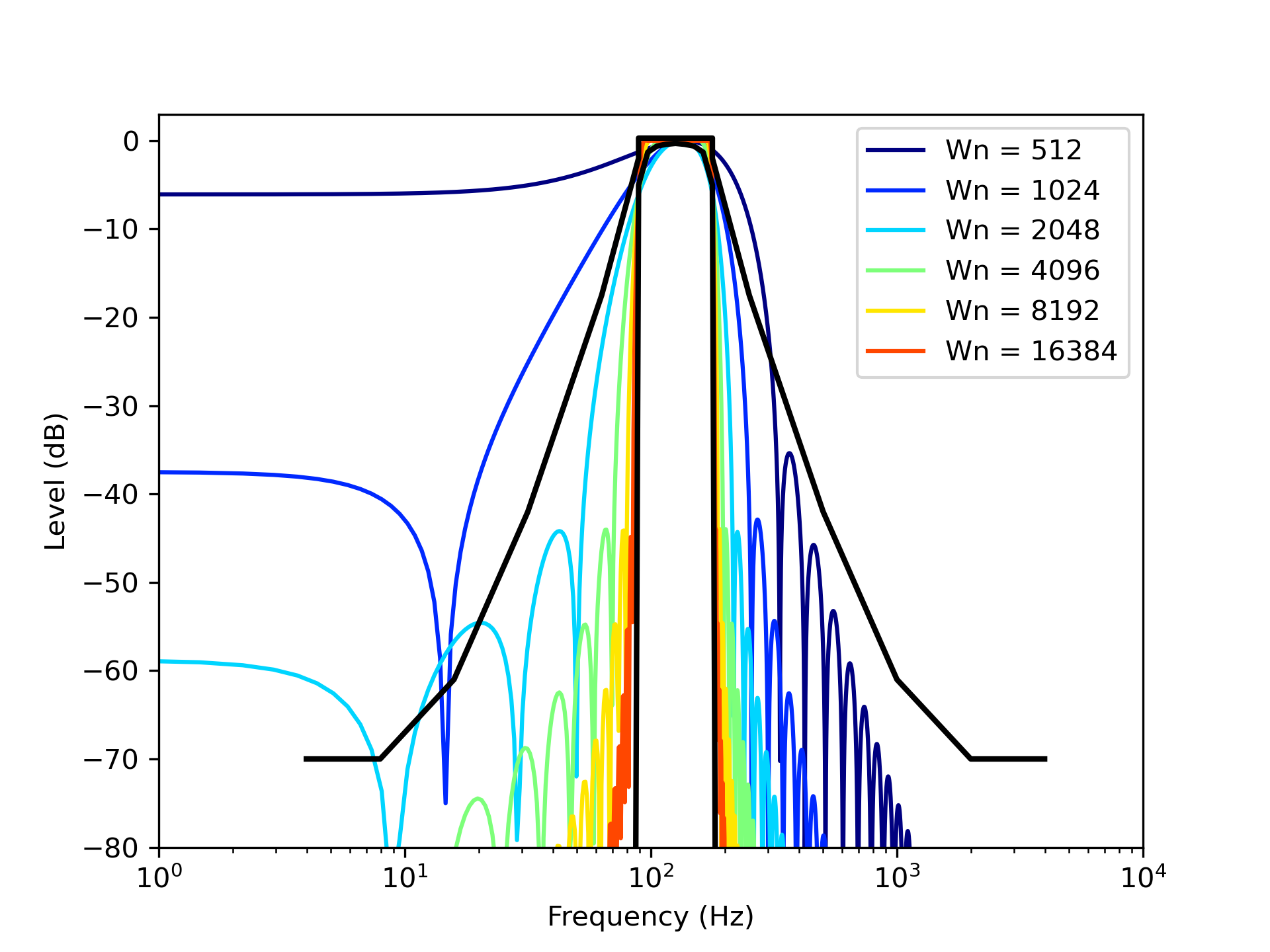
図１: 窓関数法による125 Hz帯域バンドパスフィルタの周波数特性

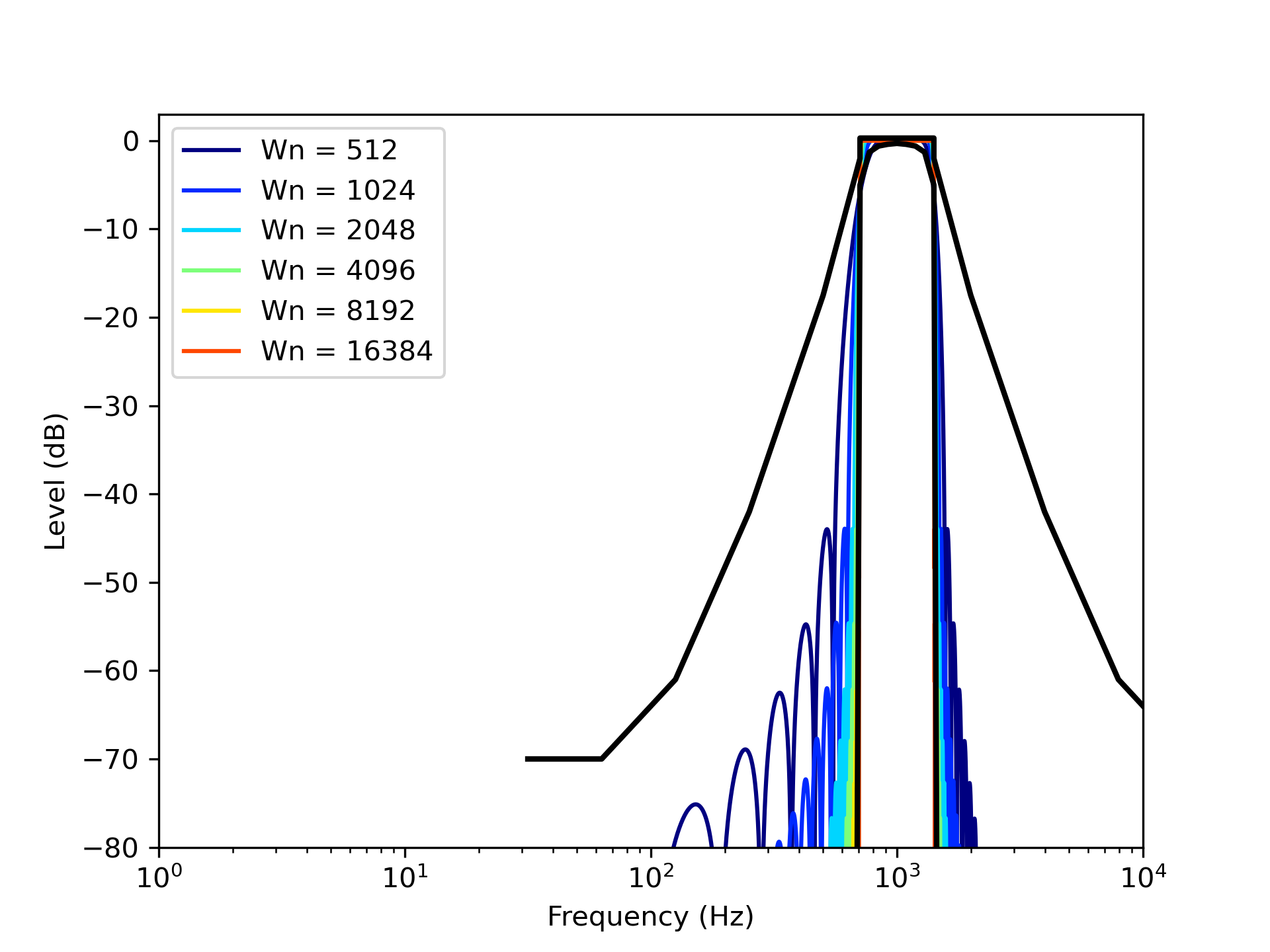
図２: 窓関数法による1 kHz帯域バンドパスフィルタの周波数特性

　次にIIRフィルタの一つであるButterworthフィルタを用いて，バンドパスフィルタを設計した。Butterworth フィルタの次数と周波数特性の関係をみてみよう。図3に125 Hz帯域オクターブバンドフィルタの周波数特性を，図4に1 kHz帯域オクターブバンドフィルタの周波数特性をそれぞれ示す。まず図3をみると，フィルタの次数が4次以上であれば十分範囲内に収まっていることがわかる。次に図4をみると，図3と形状が全く同じであり，周波数だけが1 kHzへシフトしている。このことから，IIRフィルタの次数と周波数に関係はなく，Butterworthフィルタを用いる場合は，次数が4以上であればよいことがわかる。
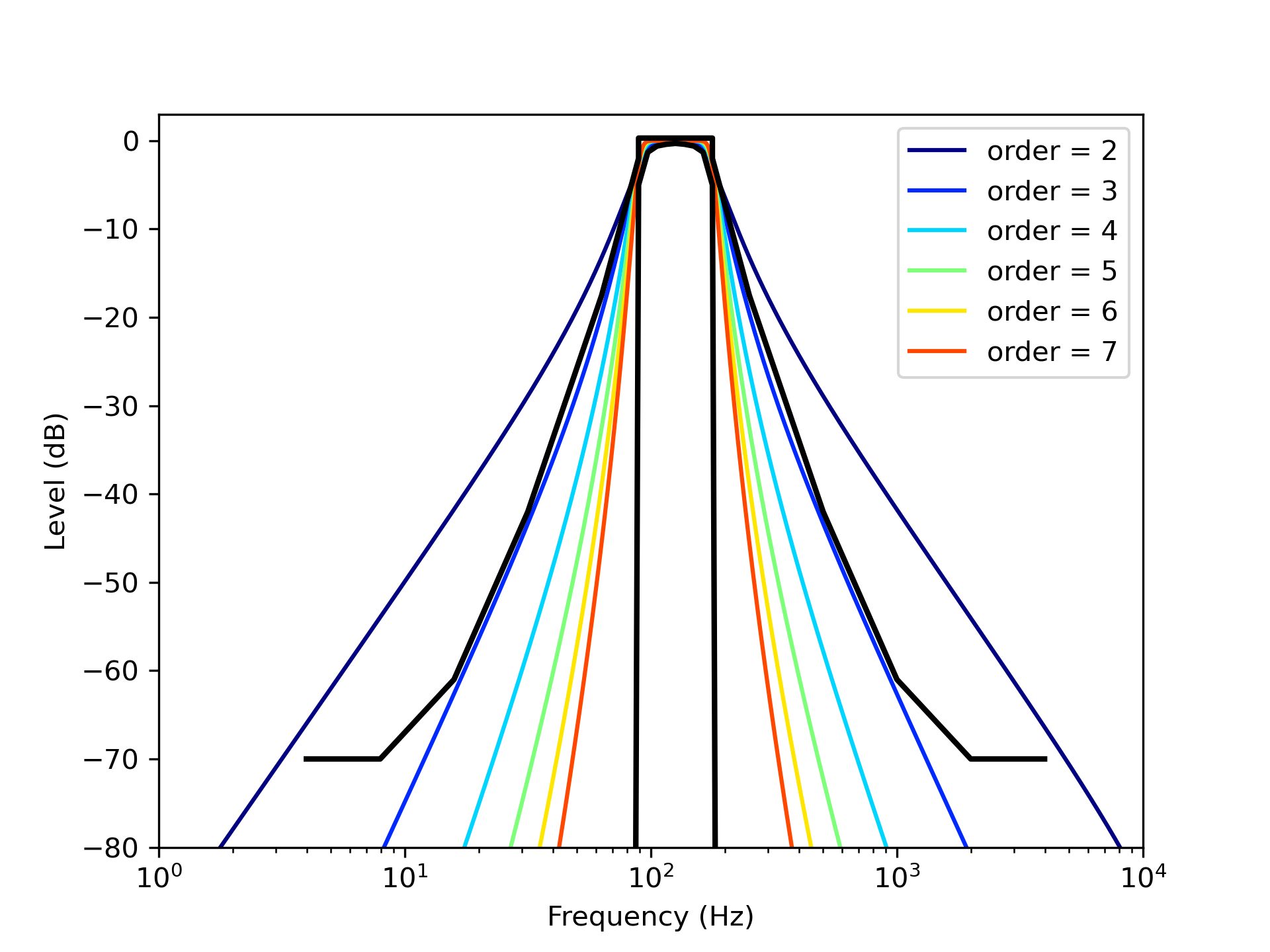
図３: Butterworthフィルタによる125 Hz帯域バンドパスフィルタの周波数特性

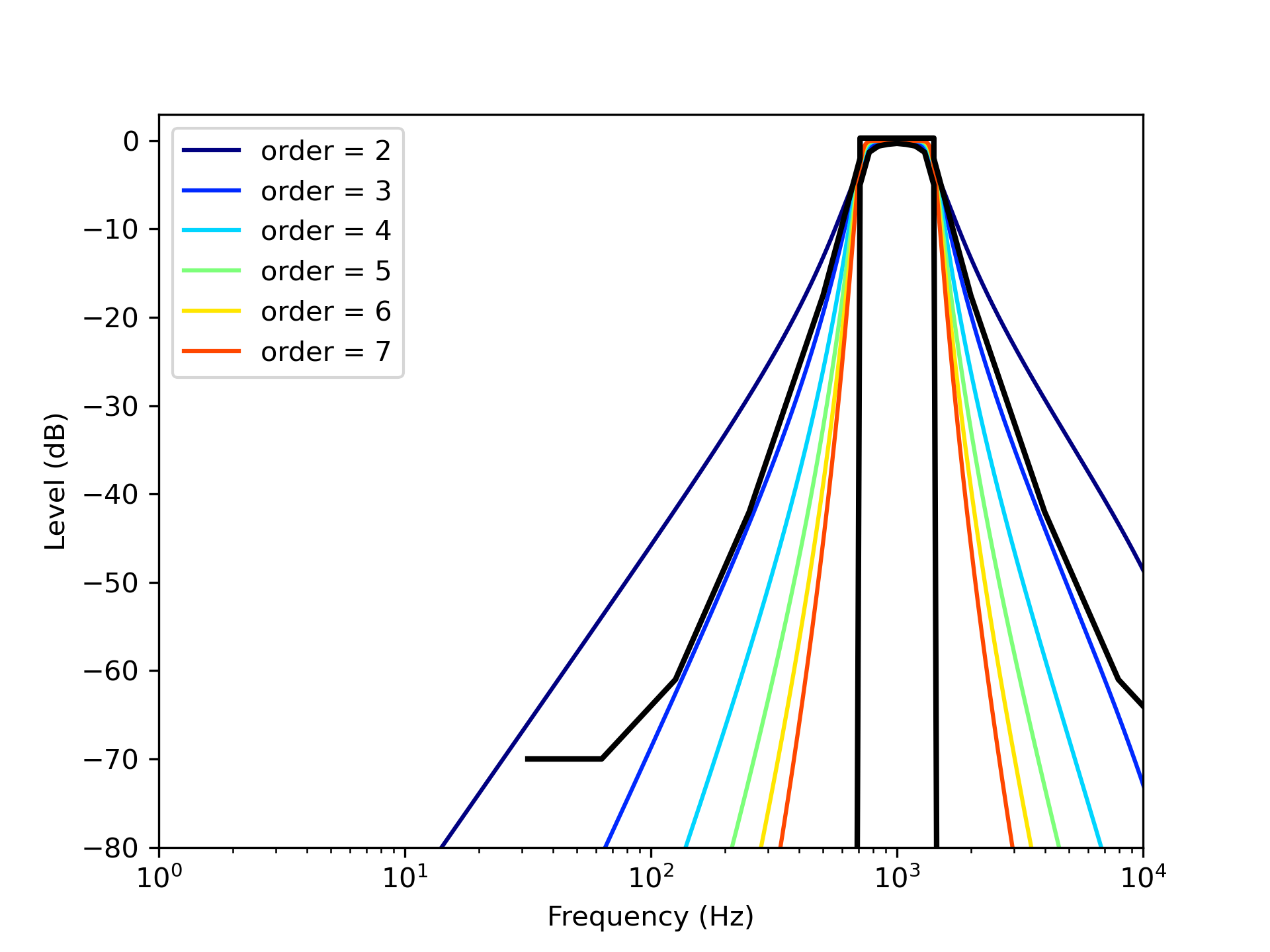
図４: Butterworthフィルタによる1 kHz帯域バンドパスフィルタの周波数特性

バンドパスフィルタがC 値に及ぼす影響

　　これらのフィルタを用いて，ベンチマーク問題A-11にあるインパルス応答のC₈₀を求めた。FIRフィルタの結果を図5に，IIRフィルタの結果を図6に示す。まずFIRフィルタの結果である図5をみると，窓の大きさが2048サンプル以上では，JND（丁度可知差異）の1 dBよりも大きな差はみられない。フィルタの周波数特性を満足する4096サンプル以上であれば，安定したC 値が得られることがわかる。次にIIRフィルタの結果である図6をみると，JNDより大きな差はみられない。このことから，フィルタの周波数特性を満足する次数が4以上であれば，安定した値が得られるといえよう。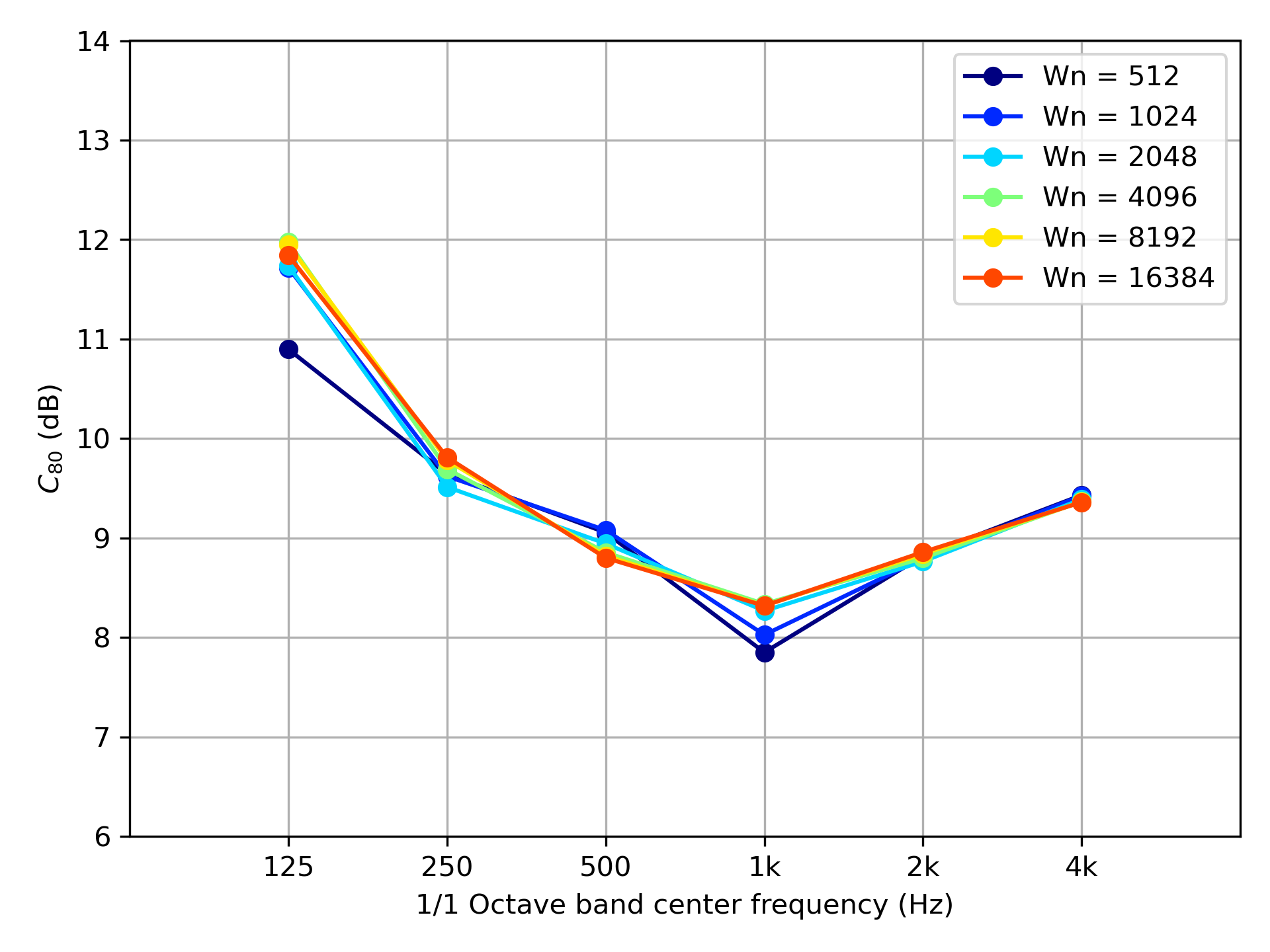
図５: FIRフィルタ（窓関数法）の窓の大きさとC₈₀の関係

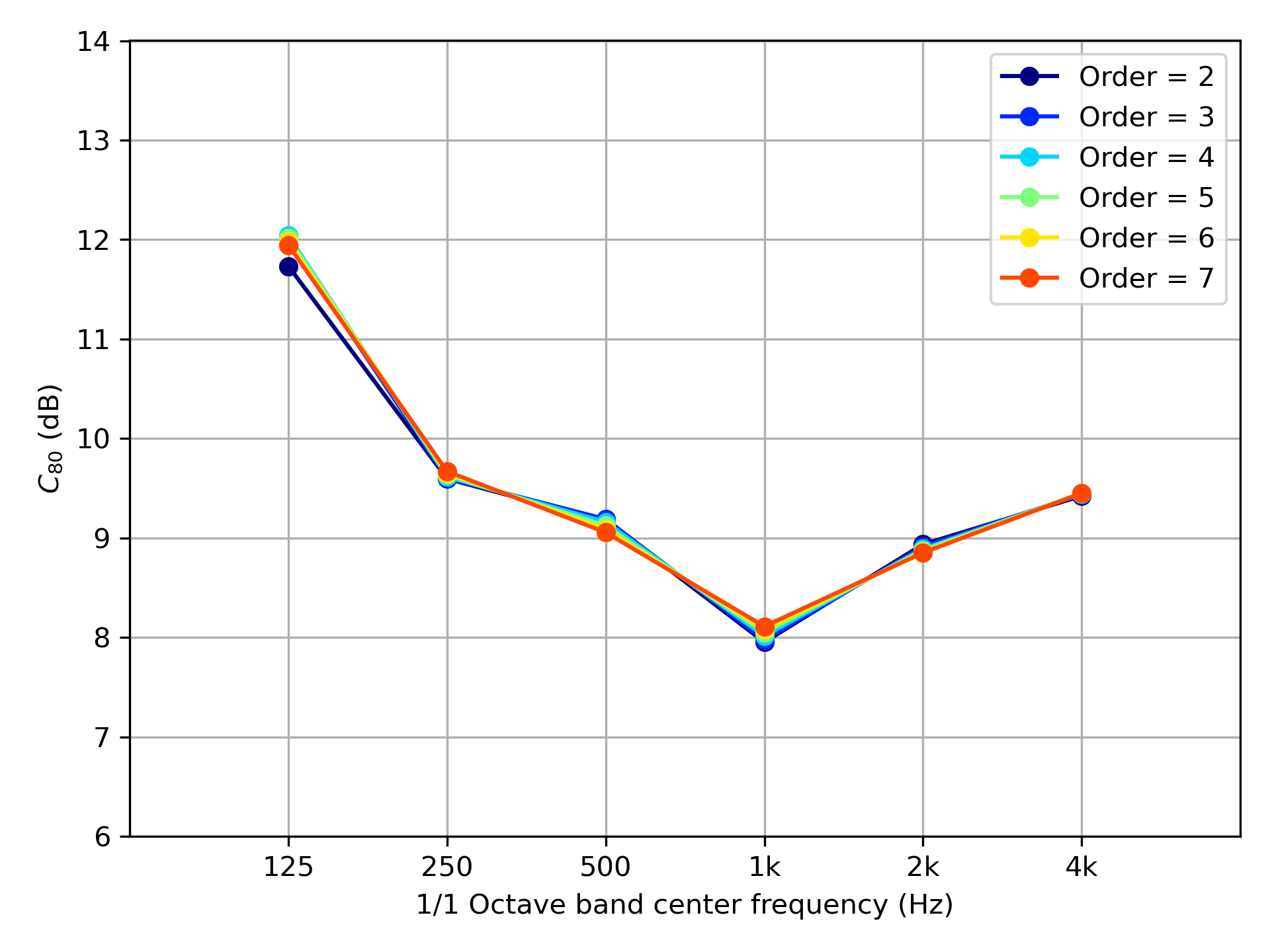
図６: IIRフィルタ（Butterworth）の次数とC₈₀の関係

おわりに

　　FIRフィルタとIIRフィルタを使ってバンドパスフィルタを設計し，フィルタの周波数特性が音響指標値の一つであるC₈₀に及ぼす影響を調べた。その結果，FIRフィルタのタップ長（ここでは窓の大きさ）は周波数と反比例の関係にあること，IIRフィルタの次数は周波数と関係がないことを確認した。また，IEC（またはJIS）規格を満足するフィルタであれば，C₈₀の差はJND以下になることがわかった。フィルタ設計の一助にしてほしい。