室内音響指標ベンチマーク

コラム２：
十分な減衰が得られない応答から残響時間を読む

はじめに

　残響時間は，逆二乗積分によって得られる減衰曲線（いわゆるシュレーダー曲線）の傾きから算出される。しかし，インパルス応答の時間長さを十分に取らなかったために，残響時間を読み取るために必要な残響減衰が得られていないことがまれにある。このような問題は，アトリウム，体育館，公共空間など，残響が長い空間でインパルス応答を収録するときに生じやすい。本コラムでは，このような応答から残響時間を推定する方法を紹介する。

データ長が残響時間の読み取りに及ぼす影響

　ベンチマーク問題B12のインパルス応答は，問題A13の応答をもとに生成されている。問題A13の応答は，ホワイトノイズを残響時間が約3.0秒になるように指数減衰させた応答で，長さ6.0 秒分のデータをもつ。問題B12の応答は，問題A13の応答から始めの 1.65 秒分を切り出したものである。そのため，残響時間が 3.0 秒程度にも関わらず，残響部分は1.65 秒分のデータしかない。問題B12のインパルス応答を図1に，1000 Hz帯域の二乗応答波形を図2に，1000 Hz帯域の残響減衰曲線を図3に示す。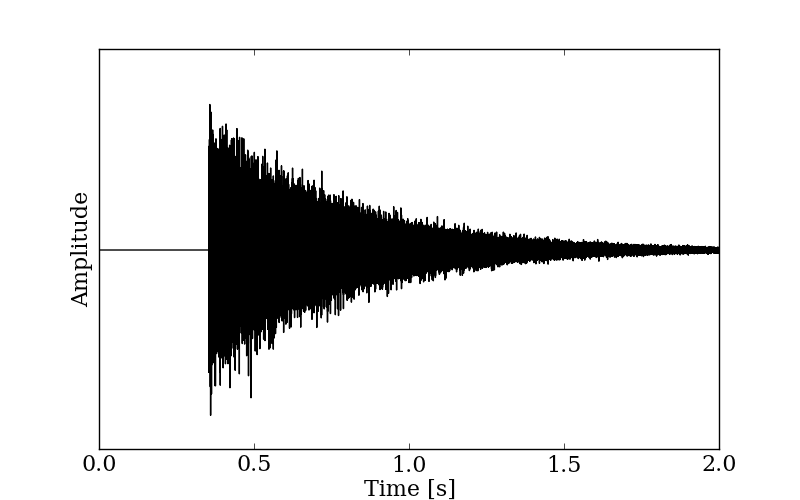
図1: ベンチマーク問題B12のインパルス応答

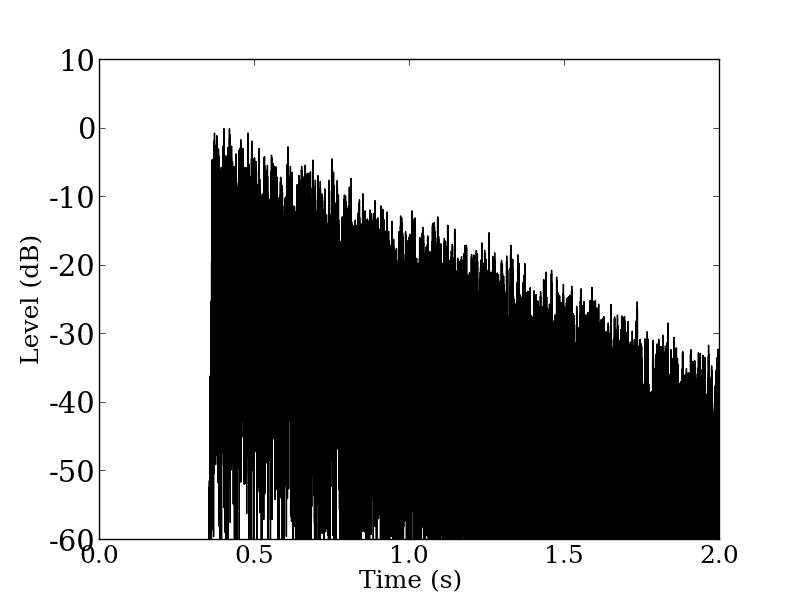
図2: ベンチマーク問題B12の二乗応答波形（1000 Hz帯域）

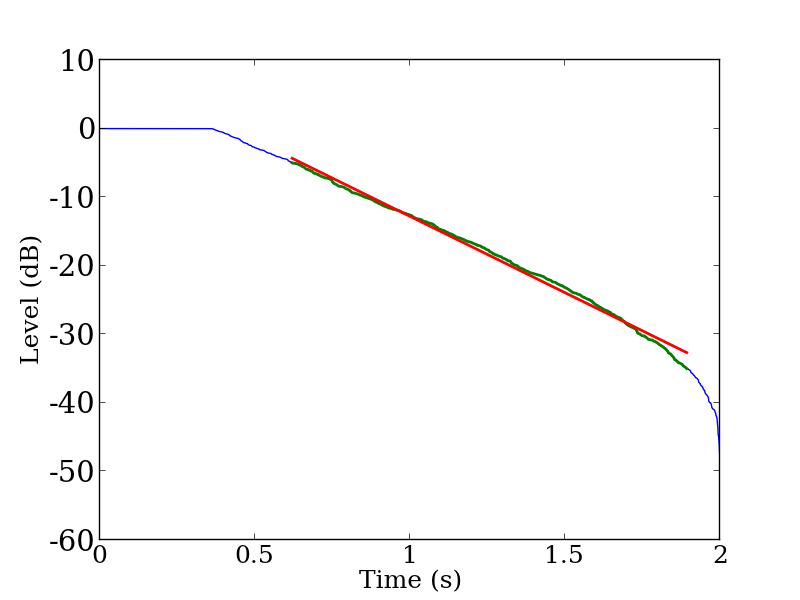
図3: ベンチマーク問題B12の残響減衰曲線（1000 Hz帯域）
（青線：残響減衰曲線，緑線：T₃₀の回帰区間の減衰曲線，赤線：回帰した直線）

　T₃₀を計測するための信号レベルは，少なくとも暗騒音より 45 dB 大きいことが望ましいと，ISO3382-1に記述されている。 これをふまえて図2をみると，暗騒音が分かるレベルまで十分減衰する前に，インパルス応答のデータが終端に至っている。信号の終端 2.0 秒に至るまでのレベル減衰は 35 dB程度であり，T₃₀を読み取るために必要な 45 dBのエネルギ減衰が確保できていないため，残響時間が適切に求めないことが予測される。
　次に図3に示す残響減衰曲線を見てみよう。データ最後の部分が急激に値が小さくなっている。これは，時系列が進むに従って積分区間が小さくなることによる。そのため，この応答の残響減衰曲線を描くと，T₃₀の回帰区間の下端値 -35 dBに至る前に（この応答では -30 dB付近から），残響減衰が凸に湾曲している。
　よって，この減衰曲線からT₃₀を求めようとすると，図 3 の赤線のように湾曲部分を含めて直線回帰するため，結果として実際の残響時間よりも短く読んでしまう。このような問題を回避するためには，回帰区間を変更し，残響減衰曲線が直線的に減衰している部分を回帰して残響時間を読む必要がある。

回帰区間の変更

　問題B12のインパルス応答は，T₃₀から残響時間を推定することが困難な応答であることがわかった。そこで，回帰区間の下端値を変更することを試みよう。既に確認しているように，図 2 をみると 35 dB程度しか減衰していない。そこで，25 dBを回帰区間の下限値と決め，–5 dB から –25 dBまでのデータを用いてT₂₀から残響時間を求めることにしよう。図 4 に回帰区間を変更して回帰直線を描いた1000 Hzの残響減衰曲線を示す。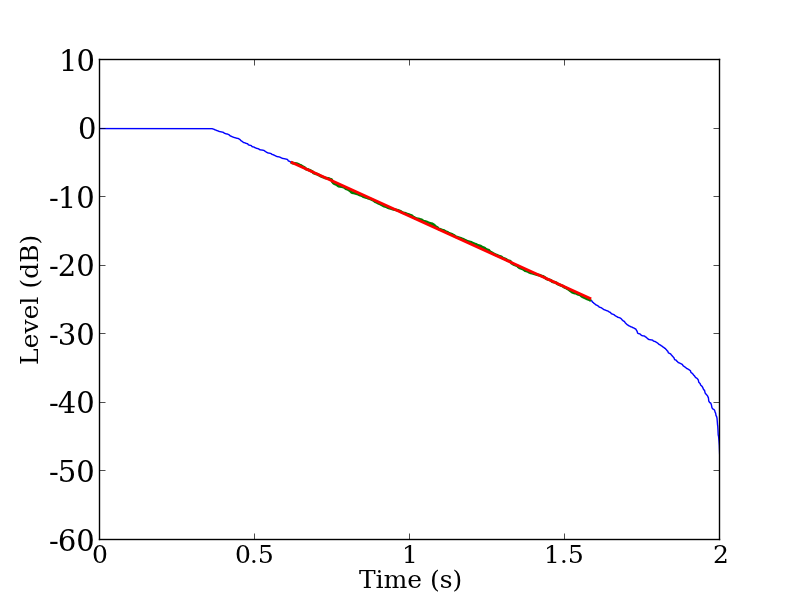
図4: 図1に示すインパルス応答の残響減衰曲線（1000 Hz帯域）
（青線：残響減衰曲線，緑線：回帰区間 –5dB から –25 dB の減衰曲線，赤線：回帰した直線）

これをみると，回帰直線は直線的に減衰する部分にほぼフィットしていることから，適切に残響時間が読めることが期待できる。問題B12の応答は，125 Hzから 4 000 Hzまで全ての帯域で約 35 dBの減衰しか得られていなかった。そこで全ての帯域において，–5 dBから –25 dBを回帰区間としてT₂₀を求めることにした。
　それでは， 問題B12のインパルス応答から求めたT₂₀, T₃₀と，問題B12の応答を作るもととなった，6.0 秒分のデータをもつ問題A13の応答から求めたT₃₀を比較してみよう。結果を図 5 に示す。
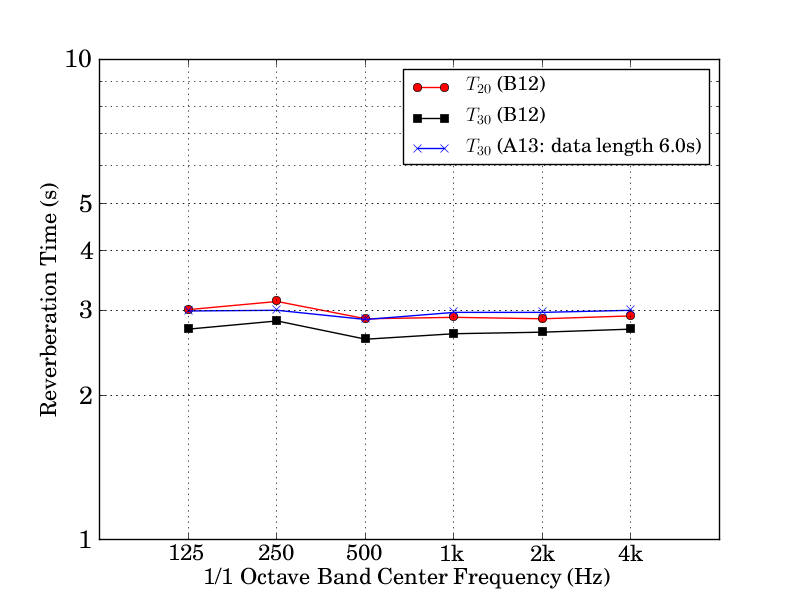
図5: 残響時間周波数特性

問題A13のインパルス応答と問題B12のインパルス応答は同じ減衰であるから，残響時間はどちらからもほぼ同じ値が読み取れることが望ましい。そこで，問題A13の応答から求めたT₃₀（青線）をリファレンスとしてみて図5をみると，問題B12の応答から求めたT₃₀（黒線）は，最大約 0.3 秒短いことがわかる。一方，問題B12の応答からも求めたT₂₀（赤線）は，最大約 0.1 秒のずれがみられるが，T₃₀よりもリファレンスに近い値である。よって，問題B12の応答から適切な残響時間を読み取るためには，T₂₀を読んだ方が良いことが確認された。

　問題B12の応答のように十分な減衰が得られてないインパルス応答から残響時間を推定するためには，回帰区間を変更することが望ましい。ただし，回帰区間を小さくすると，ちょっとした値のゆらぎが回帰直線に大きく影響する。回帰区間はなるべく大きく取るべきである。

減衰部分の時間長さと残響時間の関係

　計測時には，残響の長さを見積もって必要なデータ長さを記録しなければならない。そこで必要なデータ長さについて考えてみよう。
　残響時間は室内の音響エネルギー密度が 60 dB減衰するのに要する時間である。一方，T₃₀を求めるために必要なエネルギ減衰は 45 dBである。単純に考えれば，エネルギー減衰部分の時間は，残響時間の75 % 以上の時間が必要である。
　そこで問題A13のインパルス応答を使って，逆二乗積分の積分開始時刻を徐々に小さくしながら残響減衰曲線を描いた。積分開始時刻は 1.5 秒から 4.0 秒まで，0.25 秒間隔で変化させた。図6に問題A13のインパルス応答を，図7に 500 Hz帯域の残響減衰曲線の変化を示す。これをみると，–35 dB付近までほぼ同じ変化を示しているのは，積分開始時刻が 2.25 秒以上である。このことからも，残響減衰部分の収録時間は，残響時間の 75 % 以上なくてはならないことがわかる。もちろん，インパルス応答全体としての収録時間は，直接音到達までの時間なども含めなくてはならないから，それ以上の長さが必要であることに注意されたい。
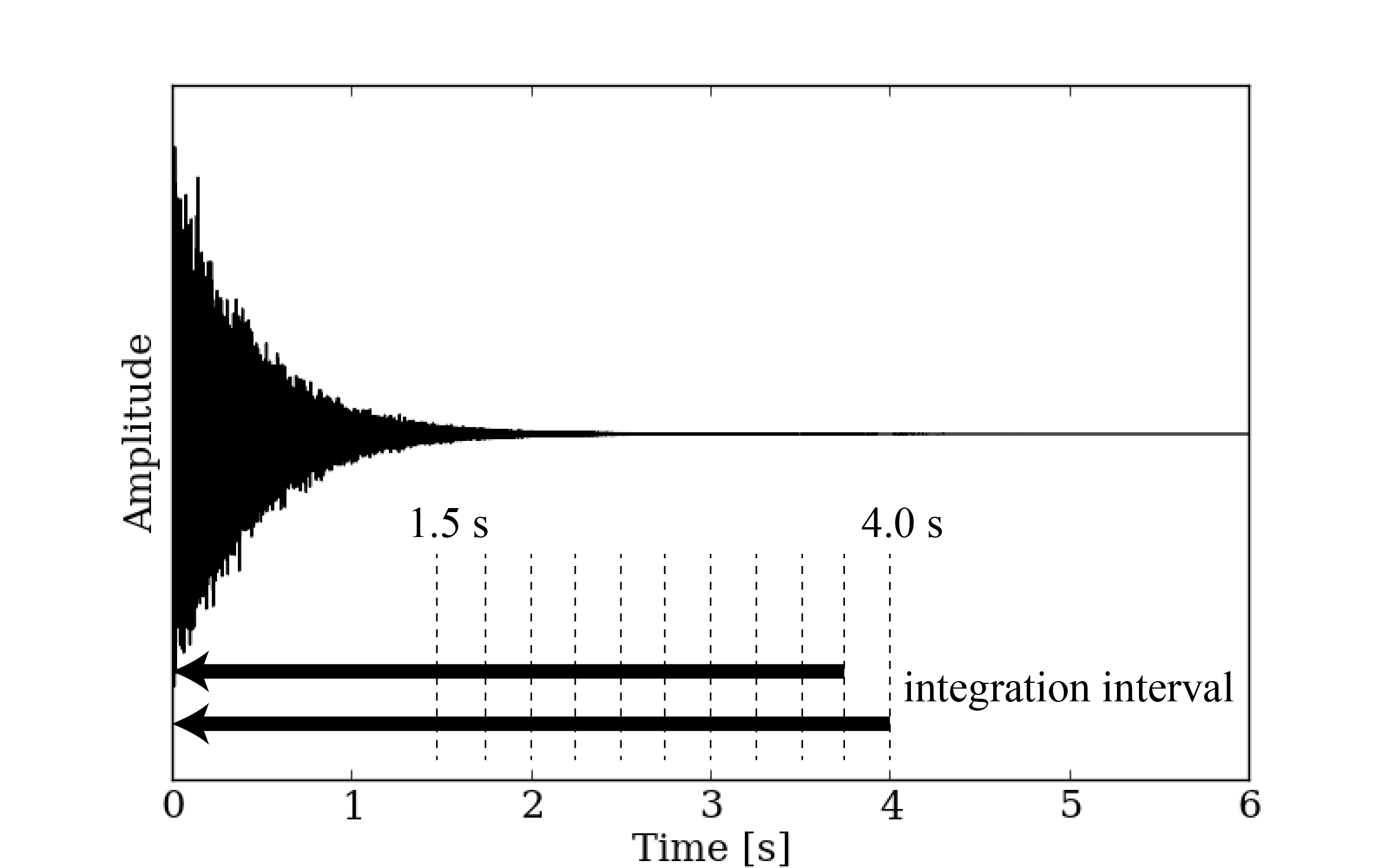
図6: 問題A13のインパルス応答


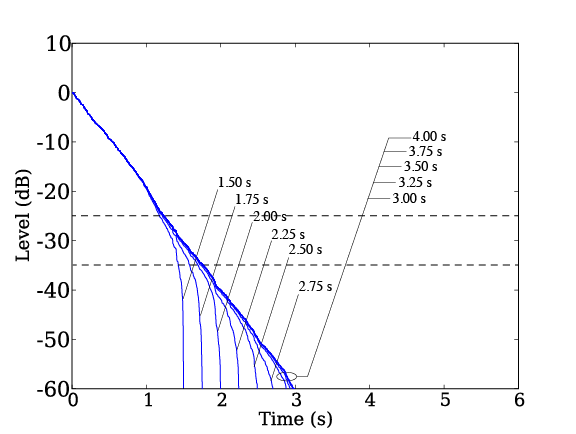
図7: 積分開始時刻を変化させた残響減衰曲線（500 Hz帯域）

対策

　はからずしも十分な減衰が得られていないインパルス応答から残響時間を推定する場合には，以下のような対策を講じるべきである。

• オクターブ帯域ごとに二乗応答波形を描き，減衰が読み取れる回帰区間のレベルを調べる。
• 解の安定性を得るために，回帰区間はできるだけ大きくとる。
• オクターブ帯域ごとに残響減衰曲線を描き，残響減衰曲線と回帰直線がフィットしているか確認する。

おわりに

　オクターブ帯域ごとに残響減衰曲線を描き，直線部分に回帰出来ているか確認することを忘れないようにしよう。