Benchmark Problems for Acoustical Parameters

Column 5:
A comparison between the design methods of digital filter and derived room acoustical index

Introduction

Considering a design method of digital filters is needed to derive room acoustical indexes. Octave band filters or 1/N-octave band filters are defined in the standards IEC61260-1 for international and JIS C1514 for Japan, and we should design digital filters referring to these standards for measuring room acoustical index. The method of designing digital filters is usually discussed in the field of digital signal processing, therefore there are few materials in the architectural acoustic field that describes the effects of digital filters for deriving room acoustical indexes. In this column, we would like to point the design method of bandpass filters (utilizing FIR or IIR filters) for deriving room acoustical indexes, and investigating the effect of the filter design method for deriving room acoustical index C₈₀ as an example.

A relation between the type of bandpass filters and their center frequency

Firstly, we would like to discuss FIR bandpass filters utilizing a window function. We use the Hanning window as a window function. Let’s see the relation between the lengths of window functions and their frequency responses. Figure 1 shows the frequency responses of 125 Hz bandpass filters and Figure 2 shows the frequency responses of 1 kHz bandpass filters. Black lines in these figures indicate the upper limit and lower limit of the frequency response of class 1 defined in IEC61260-1 (or JIS C1514). We should design our bandpass filters whose frequency responses are between the upper limit and the lower limit.
It is needed to use the size of the window function over 4096 samples from the result shown in figure 1. On the other hand, we can find that the size of 512 samples is enough from the results shown in figure 2. Therefore, it is obvious that the size of 8192 samples is needed in 63 Hz band and the size of 16384 samples is needed in 31.5 Hz band in the case of designing FIR filters utilizing window function because the required window size and frequency (bandwidth) have an inverse relation.
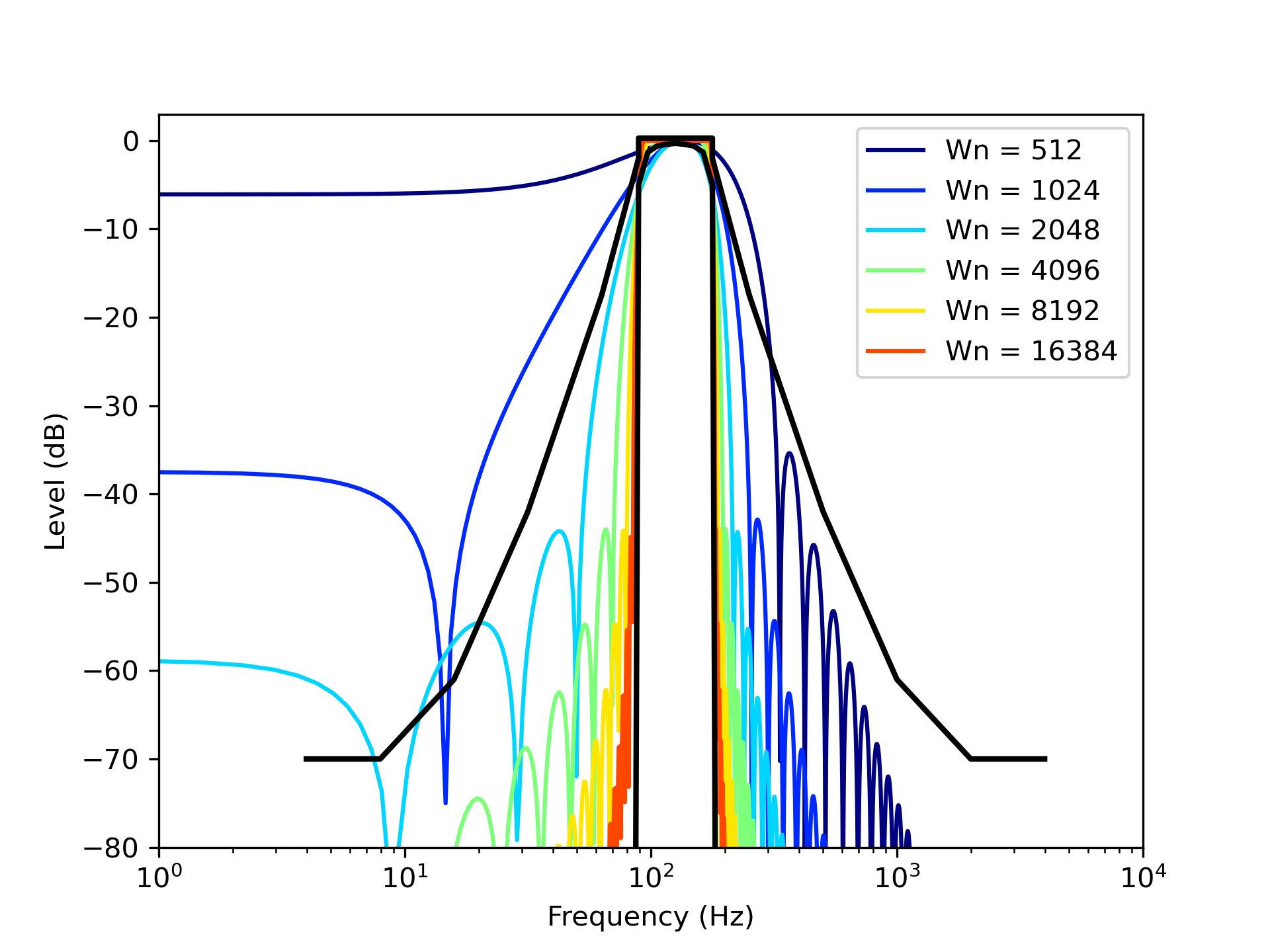
Figure 1: Frequency response of 125 Hz bandpass filters designed by window function method.

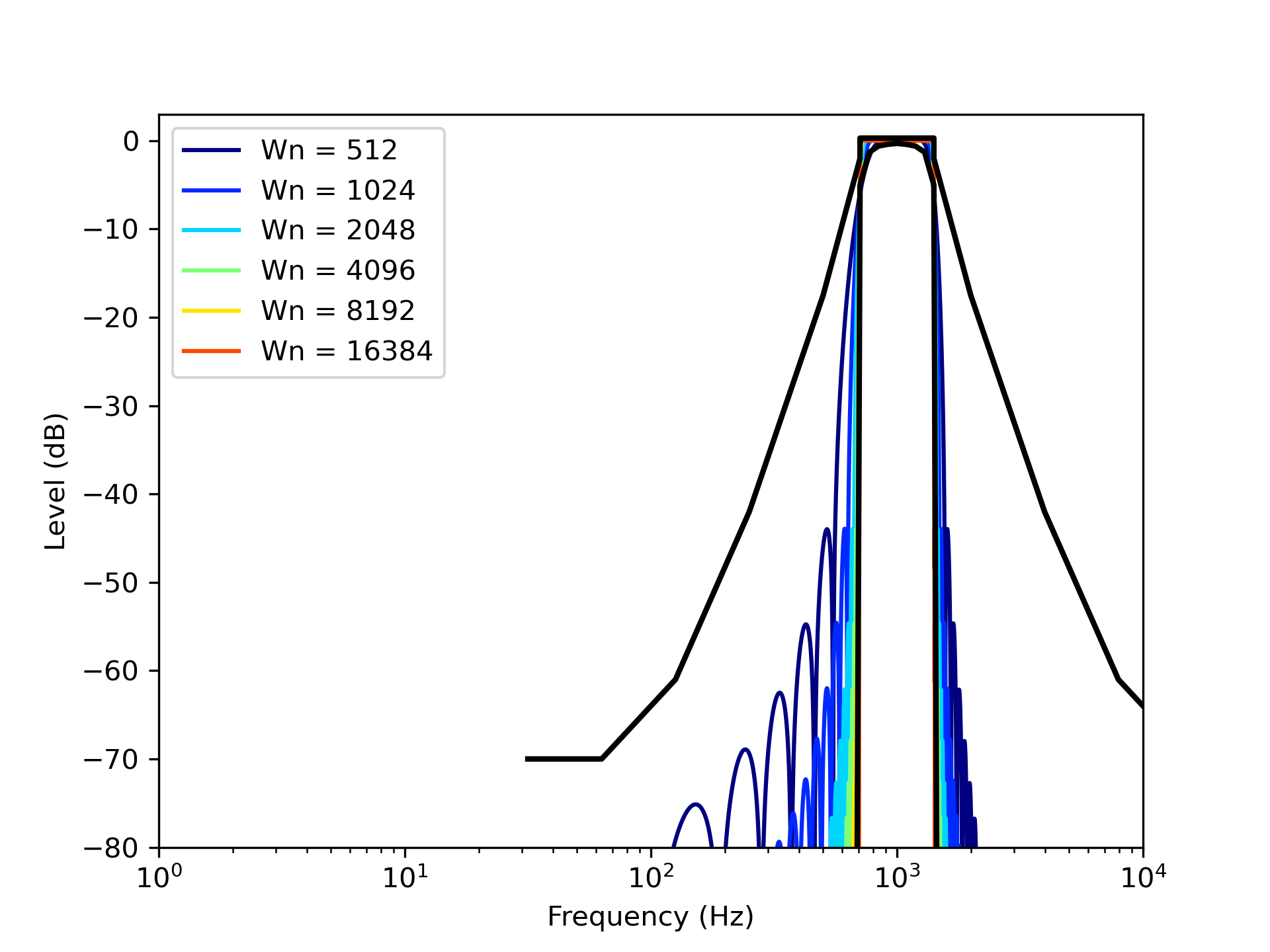
Figure 2: Frequency response of 1 kHz bandpass filters designed by window function method.

Next, let’s see the relation between the number of orders of Butterworth filters (one of IIR filters) and their frequency responses. Figure 3 shows the frequency responses of 125 Hz bandpass filters and Figure 4 shows the frequency responses of 1 kHz bandpass filters. The filters whose number of orders exceeding 4 is enough because their frequency responses are within the upper limit and lower limit as we can see in figure 3. In figure 4, the shape of responses is the same as the responses in figure 3, they are just shifted to 1 kHz band in the frequency domain. Therefore the IIR bandpass filters higher than 4th order fulfills our requirement if we use Butterworth filters.
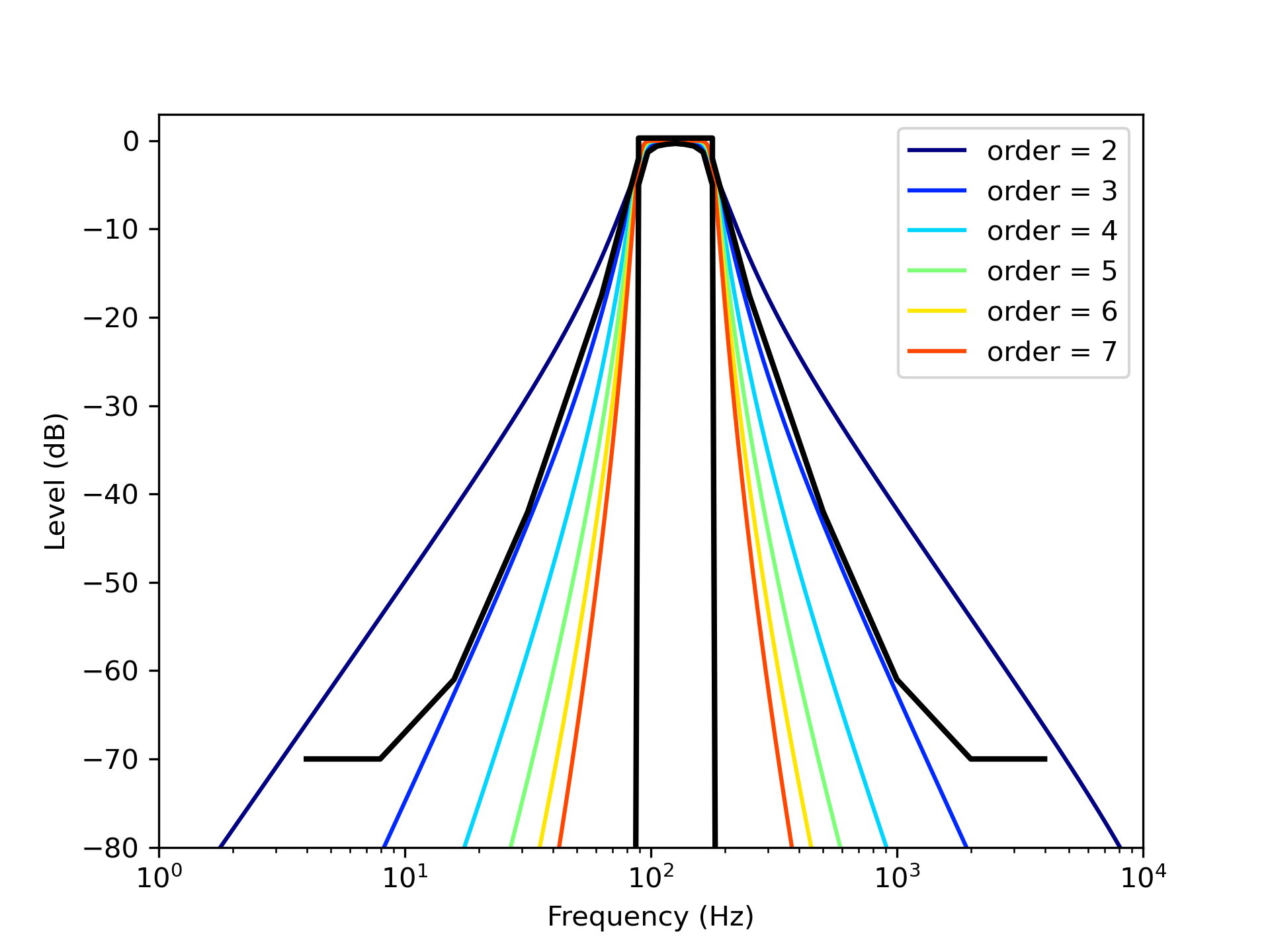
Figure 3: Frequency response of Butterworth filters in 125 Hz frequency band.

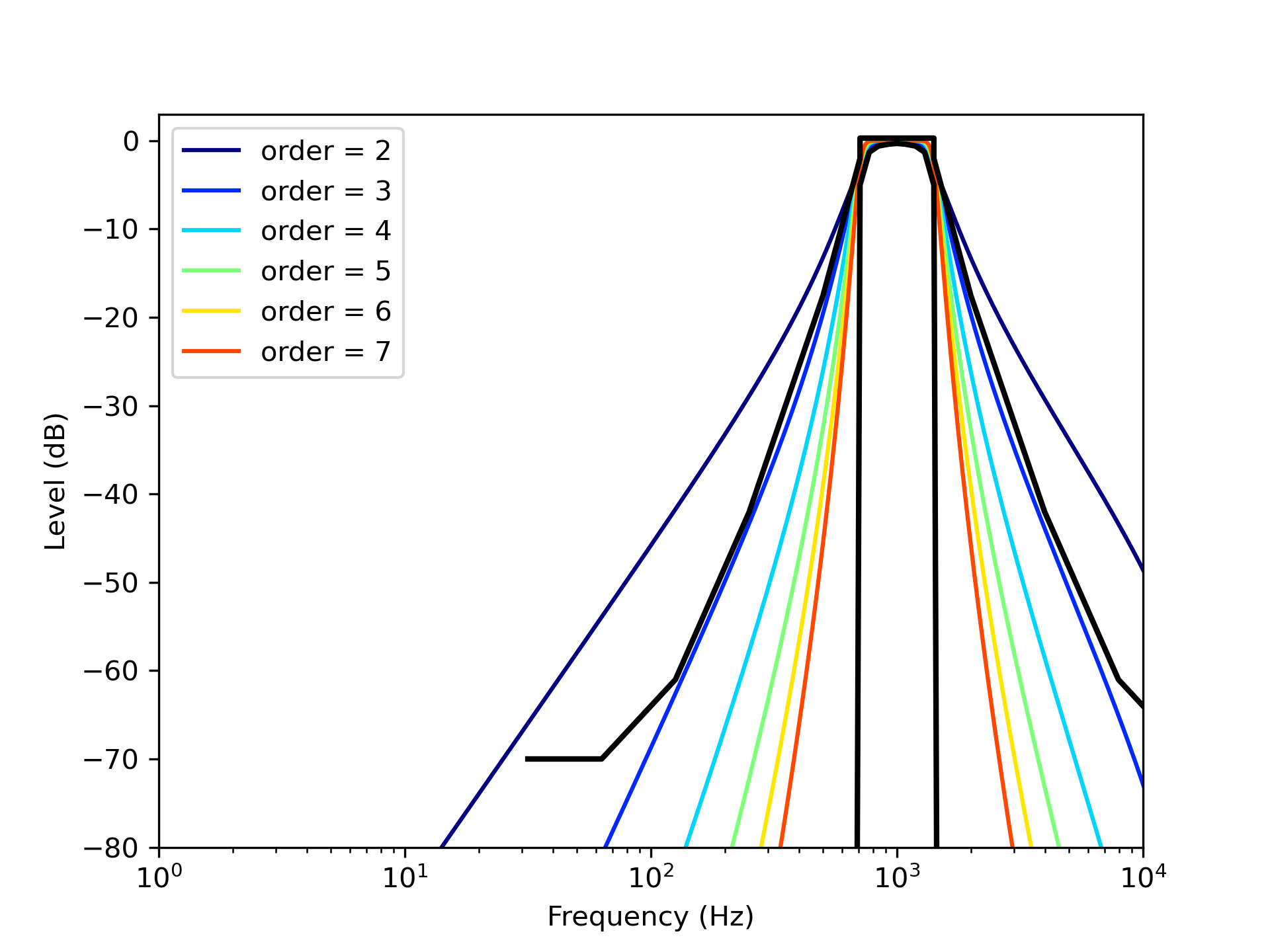
Figure 4: Frequency response of Butterworth filters in 1 kHz frequency band.

The effect of properties of bandpass filters for deriving C value

　　Using the filters mentioned above, we calculate the C80 value of the impulse response shown in benchmark data A-11. The results utilizing FIR filters are shown in figure 5, and the results utilizing IIR filters are shown in figure 6. From the results in figure 5, we cannot recognize differences greater than 1 dB (JND (just noticeable differences) of C₈₀ value) when we use the FIR filters whose size of the window is over 2048. From the results utilizing IIR filters in figure 6, we cannot see the differences over the JND of the C₈₀ value. We can get a certain C₈₀ value if we use IIR bandpass filters whose number of orders is over 4.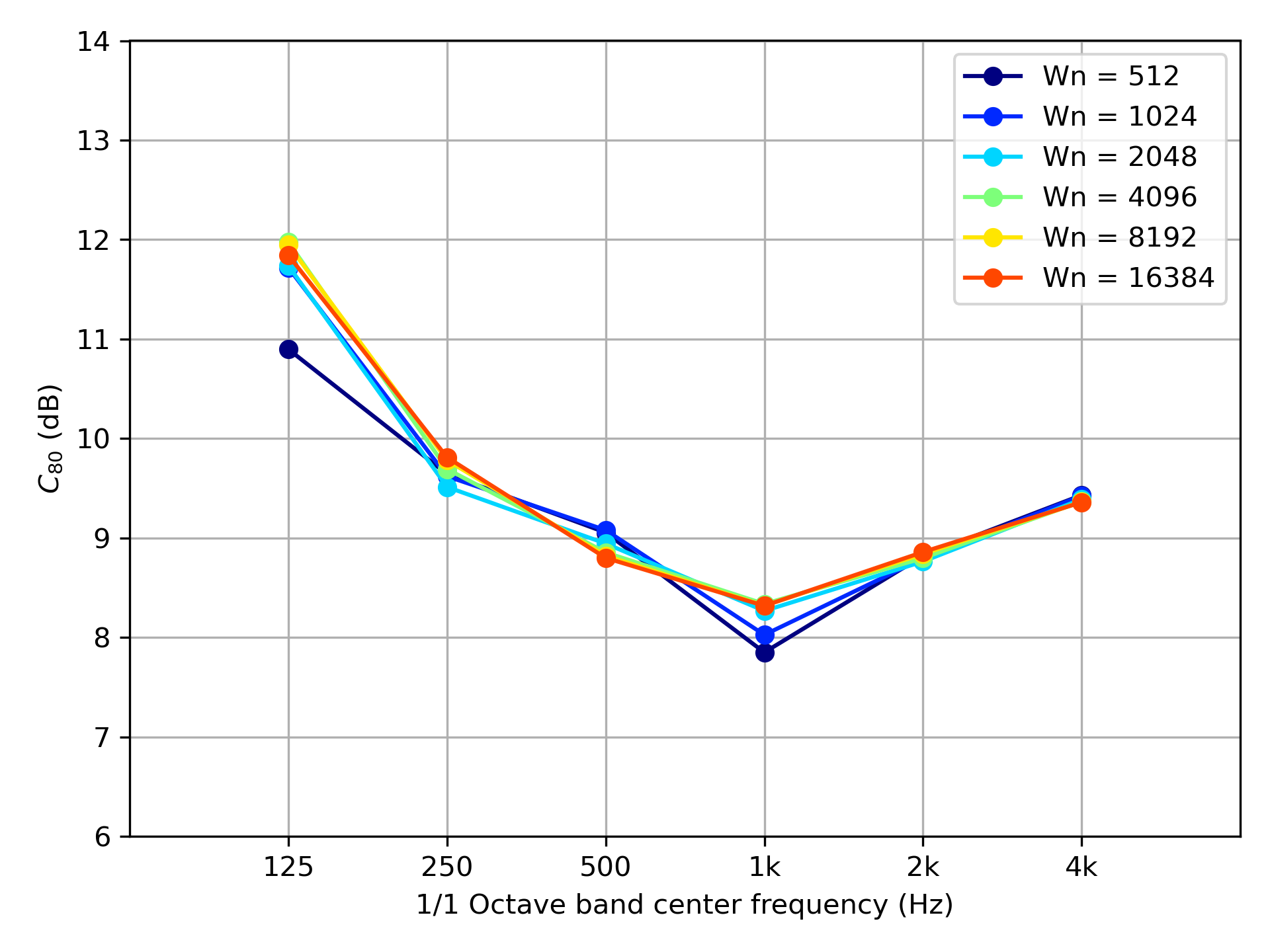
Figure 5: The relation between the size of FIR filters and derived C₈₀ values.

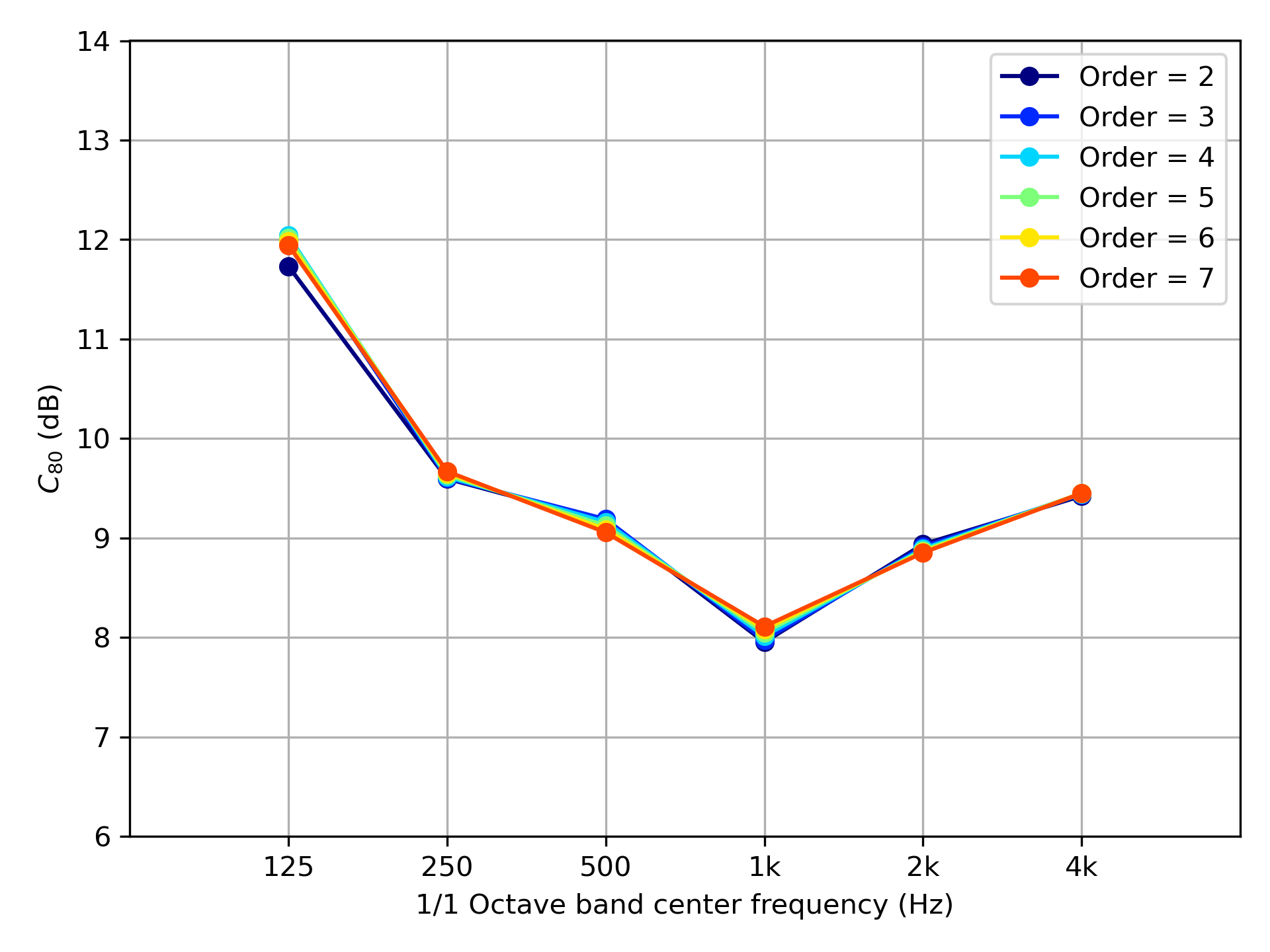
Figure 6: The relation between the number of orders of IIR filters (Butterworth filters) and derived C₈₀ values.

Conclusion

The effect of the FIR filter or IIR filter design method for deriving the C80 value is introduced in this column. We found that the required window size and frequency (bandwidth) have an inverse relation and there is no effect from the number of orders of IIR filters to the frequency responses. We can derive a certain C₈₀ value if we use filters whose properties satisfy the definitions in IEC or JIS standards. We hope this information will be of your help when designing digital filters for deriving room acoustical indexes….