EA法による吸音特性の測定
EA法による測定原理について概要を示す。詳細は文献[1]を参照されたい。
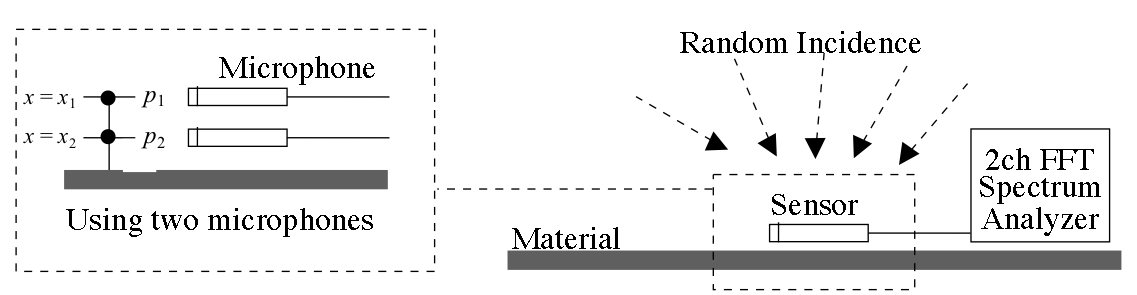
Fig. 1 EA法による測定におけるマイクホロン，試料の位置関係
Fig.1にEA法の測定系のブロックダイアグラムを示す。この手法は，材料への音波の入射条件としてランダム入射を想定し，材料表面近傍に設置した2本のマイクロホンもしくは音圧-粒子速度センサーで測定される伝達関数からノーマル（垂直方向）音響インピーダンスを求める手法である。 材料へランダム入射する音源を使用し，材料境界からの特定の反射波の影響をキャンセルできるため，材料寸法に依存しない安定した測定値がえられる。また，上記マイクロホンや音圧-粒子速度センサを材料表面近傍に設置するため，ランダム入射する音源を仮定しているにも関わらず，比較的小さな測定対象への適用も可能である。 以下，2本のマイクロホンを用いる場合の算出方法について示す。
材料表面における音圧反射係数は下記のように与えられる。
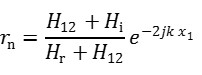
ここで
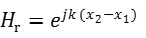
である。H12は、２つのマイクロホンにより測定した複素音圧p1，p2の比を取ることにより求められる伝達関数である。
導出
Fig. 1において、試料へ入射する複素音圧piを、時間項を省略して下記とおく。
・・・・・・・・・・(1)
試料における反射音圧prは、音圧反射係数rnを用いて下式のように表せる。
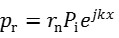・・・・・・・・・・(2)
2つのマイクロホン位置における音圧p1，p2は、正負方向それぞれに進む音波の重ね合わせとして、それぞれ下式のように表せる。
・・・・・・・・・・(3)
・・・・・・・・・・(4)
2点における音圧の比を取ることにより、それらの伝達関数H12は下記のように表せる。
・・・・・・・・・・(5)
上式をrnについて解くと
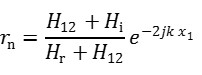・・・・・・・・・・(6)
と表せる。ここで
・・・・・・・・・・(7)
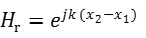・・・・・・・・・・(8)
であり、両点の距離x1-x2により計算できるので、伝達関数H12およびx1が分かれば、音圧反射係数rnを求めることができる。
垂直方向の比音響インピーダンス比および垂直入射吸音率は下記のように与えられる。
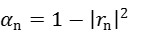
ここでZ0は空気の特性インピーダンスを表す。
参考文献
[1]Toru Otsuru, Reiji Tomiku, Nazli Bin Che Din, Noriko Okamoto and Masahiko Murakami，"Ensemble averaged surface normal impedance of material using an in-situ technique: Preliminary study using boundary element method"，Journal of Acoustical Society of America，Vol. 125，No. 6，pp.3784–3791 (2009)．